cloud edwards
Member
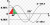
So, How does one find the total shaded area (red and green in the attachment).
I'm unsure whether the first half (red part) is going to be the integral of sinx or (cosx -sinx)
My instinct working out for total area of the shaded:
integration of sin x between 0 and 45 + [integration of sinx -cos x in between 45 to 90]
I'm unsure whether the first half (red part) is going to be the integral of sinx or (cosx -sinx)
My instinct working out for total area of the shaded:
integration of sin x between 0 and 45 + [integration of sinx -cos x in between 45 to 90]
Attachments
-
93.3 KB Views: 71