Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Math/Physics (1 Viewer)
- Thread starter Cujo10
- Start date
What do you mean by solve? What are you talking about?Using two formulas to find 2 unknowns called system of equations ? if so, how would you solve f=ma if m and a are unknown ?
Cujo10
Member
- Joined
- Dec 15, 2017
- Messages
- 121
- Gender
- Male
- HSC
- 2019
- Uni Grad
- 2024
Just say M=10 and A is the unknown you can solve it for F but when M and A are unknown how to you solve it. My friend and physics told me that it can be solves for the unknowns using systems of equations, but i never learnt that. For F=MA to solve for two unknown you need to use two other equation M=F/A and A=F/M its called systems equations i think.
HoldingOn
Active Member
I think he might be referring to what we would call 'simultaneous equations'. Are these in the general maths syllabus? Surely they are.
With simultaneous equations and multiple unknowns, you need several pieces of information. Generally you need one equation for each unknown quantity. So if you have two unknowns you need two equations.
And you can't "cheat" by rearranging the first equation and using that as the second, because when you try to solve it you will end up getting an equation like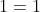 or
or 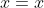 that is as useless as it is true.
that is as useless as it is true.
For example the equation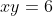 has infinitely many possible solutions for
has infinitely many possible solutions for 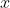 and
and 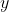 , so you need more information to go off.
, so you need more information to go off.
Suppose you are then given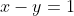 .
.
So now you have two equations:

We can rearrange the second equation, giving us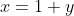 and then we can substitute this back into the first equation, giving:
and then we can substitute this back into the first equation, giving:
 = 6)
And from there it is possible to solve for . Once you know
. Once you know  you can then solve for
you can then solve for 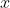 .
.
______________________________________________________________________________________________________
In some more common cases it may be better to add the equations together:


Or subtract them:


But ultimately what you're trying to do is to focus on one variable by creating an equation without all the others. Once you have that variable you can use it to find the other(s).
And you can't "cheat" by rearranging the first equation and using that as the second, because when you try to solve it you will end up getting an equation like
For example the equation
Suppose you are then given
So now you have two equations:
We can rearrange the second equation, giving us
And from there it is possible to solve for
______________________________________________________________________________________________________
In some more common cases it may be better to add the equations together:
Or subtract them:
But ultimately what you're trying to do is to focus on one variable by creating an equation without all the others. Once you have that variable you can use it to find the other(s).
Last edited:

