-
Looking for HSC notes and resources? Check out our Notes & Resources page
Please help with this question (1 Viewer)
- Thread starter kpad5991
- Start date
Infinity.What is the volume of the solid generated when the area of the curve y=3-3^x is rotated about the x axis
If bounds are given, use the formula
and use
(remember to give your answers in cubic units!)
Last edited:
dan964
what
Herowise one of your coefficients is not correct.
Might be easier to use change of base before integrating. Also maybe leave the exponent as x rather than x+1 before integrating. Less likely to make mistakes that way.
I'll do an improper integral here:
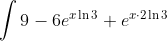
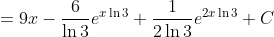
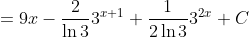
or
 \ln 3} + e^{x \cdot 2\ln 3})
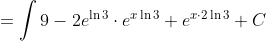

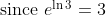
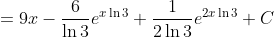
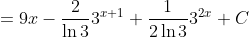
This is the improper integral. The integral with limits is done in a similar fashion.
that is some funky integration going on there:Well to summ wat the above posts states is the
x = e ^ (lnx)
is the same thing right?
didnt finish it fully, should be right if i didnt make silly errors, but you want to reach there

Might be easier to use change of base before integrating. Also maybe leave the exponent as x rather than x+1 before integrating. Less likely to make mistakes that way.
I'll do an improper integral here:
or
This is the improper integral. The integral with limits is done in a similar fashion.
Last edited:
HeroWise
Active Member
- Joined
- Dec 8, 2017
- Messages
- 353
- Gender
- Male
- HSC
- 2020
Pfft i feel dumb, i see where i went wrong, thanks a lot anyway @dan964
EDIT: Wait, no i got the same result as yours @dan964, but i didnt simplify it. if i had, it would come down to your answer, and the ordinates, as i said, im geussing the question is asking for first quadrant, i remember a similar question while going over the Cambridge book, so i just "geussed". That isnt really good but i think the working should suffice the OP
EDIT: Wait, no i got the same result as yours @dan964, but i didnt simplify it. if i had, it would come down to your answer, and the ordinates, as i said, im geussing the question is asking for first quadrant, i remember a similar question while going over the Cambridge book, so i just "geussed". That isnt really good but i think the working should suffice the OP
Last edited:
This is what I got you will see the question from the textbook and my solutions I can't seem to get 13c. The books solution is pi(9-8/log3) u^3Herowise one of your coefficients is not correct.
that is some funky integration going on there:
Might be easier to use change of base before integrating. Also maybe leave the exponent as x rather than x+1 before integrating. Less likely to make mistakes that way.
I'll do an improper integral here:
or
This is the improper integral. The integral with limits is done in a similar fashion.
https://imgur.com/gallery/u5PCA
Can someone please write the full solution to 13c
HeroWise
Active Member
- Joined
- Dec 8, 2017
- Messages
- 353
- Gender
- Male
- HSC
- 2020
Can you tell us the ordinates then, because as the working out provided by both @dan964 and i are elligible, so just put in the ordinates like normal integration, or provide us with ordinates; thatd be helpful for us ty
or send a pic of the whole excercise
or send a pic of the whole excercise
