-
Looking for HSC notes and resources? Check out our Notes & Resources page
Can someone please help with q22, 23 and 24 (1 Viewer)
- Thread starter kpad5991
- Start date
22)

Find the area of the sector and subtract it from the area of the triangle
and subtract it from the area of the triangle  .
.
_________________________________________________________________________________________
23)
a) The arc is equal to the circumference of the cone's base. With that information you can calculate the radius.
is equal to the circumference of the cone's base. With that information you can calculate the radius.
b) Once you know the slanted height of the cone and its base's radius, you can form a triangle to calculate the perpendicular height.
c) Use the volume formula for a cone.
d) The curved surface area is equal to the area of the sector .
.
_________________________________________________________________________________________
24)

a) First calculate the area of the sector in terms of
in terms of  and
and 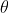 . Then express
. Then express  in terms of
in terms of 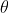 by using the perimeter and the arc length formula.
by using the perimeter and the arc length formula.
b) Differentiate the area formula and identify its maximum value. The domain should be , but it might not matter either way.
, but it might not matter either way.

Find the area of the sector
_________________________________________________________________________________________
23)
a) The arc
b) Once you know the slanted height of the cone and its base's radius, you can form a triangle to calculate the perpendicular height.
c) Use the volume formula for a cone.
d) The curved surface area is equal to the area of the sector
_________________________________________________________________________________________
24)

a) First calculate the area of the sector
b) Differentiate the area formula and identify its maximum value. The domain should be
Gonna need a bit more information.... what question?How is the solution 4/3 (4pi -3 root 3) i got 4/3(2 Pi - 3 root 3)
Sorry q22Gonna need a bit more information.... what question?
integral95
Well-Known Member
- Joined
- Dec 16, 2012
- Messages
- 779
- Gender
- Male
- HSC
- 2013
Q2222)

Find the area of the sectorand subtract it from the area of the triangle
.
_________________________________________________________________________________________
23)
a) The arcis equal to the circumference of the cone's base. With that information you can calculate the radius.
b) Once you know the slanted height of the cone and its base's radius, you can form a triangle to calculate the perpendicular height.
c) Use the volume formula for a cone.
d) The curved surface area is equal to the area of the sector.
_________________________________________________________________________________________
24)

a) First calculate the area of the sectorin terms of
and
. Then express
in terms of
by using the perimeter and the arc length formula.
b) Differentiate the area formula and identify its maximum value. The domain should be, but it might not matter either way.
OA = OB = 4cm
