dan964
what
Welcome to the 2017 HSC 2U Marathon,
1. Only post questions within the level and scope of 2U HSC Mathematics.
2. Provide neat working out when possible
3. Don't flood the thread with multiple unanswered questions/spam.
4. Challenging questions that a 2U student can pick up easily are okay, but try to stay within the 2U syllabus content.
Here is a question I've pulled for you (modified from Ascham 2011 2U trial HSC)
For the curve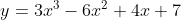
1. Find the stationary points and determine their nature
2. Find any points of inflexion
3. Sketch the graphs showing info from (1) & (2)
4. When is the curve decreasing with downward concavity?
1. Only post questions within the level and scope of 2U HSC Mathematics.
2. Provide neat working out when possible
3. Don't flood the thread with multiple unanswered questions/spam.
4. Challenging questions that a 2U student can pick up easily are okay, but try to stay within the 2U syllabus content.
Here is a question I've pulled for you (modified from Ascham 2011 2U trial HSC)
For the curve
1. Find the stationary points and determine their nature
2. Find any points of inflexion
3. Sketch the graphs showing info from (1) & (2)
4. When is the curve decreasing with downward concavity?
