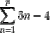poppyisloveinthewind
New Member
- Joined
- Apr 21, 2017
- Messages
- 15
- Gender
- Female
- HSC
- 2018
1+6+11+...+(5p-4)
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
was this done through trial and error
or, if you prefer:
or even:

No no - not by trial-&-error. As I am very well-versed with the use of the sigma notation, this is nothing to me. It may take you a while to get used to it. Don't be discouraged.was this done through trial and error
I thought it was +5 for some reason and hence couldnt solve itNo no - not by trial-&-error. As I am very well-versed with the use of the sigma notation, this is nothing to me. It may take you a while to get used to it. Don't be discouraged.
was this done through trial and error
In simple terms, you need to recognise that the sequence is arithmetic, which can be proven by checking that T2 - T1 = T3 - T2.right i think i get it now, the answer is in the question and by using the last value you have to do trial and error, am i right?