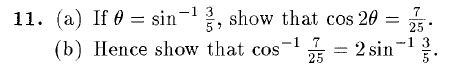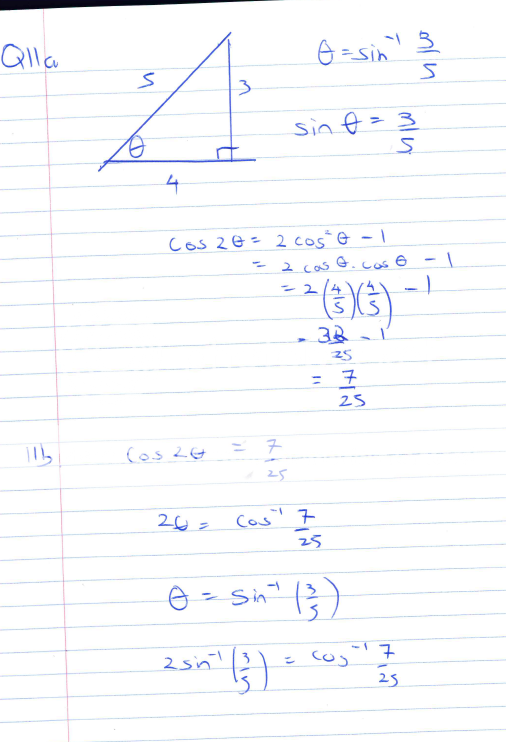davidgoes4wce
Well-Known Member
Seeing that we have a thread open for Year 11 3 Unit Cambridge, I have decided to open up a thread for Year 12 3 Unit Cambridge for all discussion on questions that students are working on.
I'll kick the ball rolling
EXERCISE 2A
Q5j
Been spending only 3 minutes on this but i got my final answer in radians, not exact value, as required in the question.
-1}}{1-2sin^{2} \frac{\pi}{10}} )
}{ cos({\frac{\pi}{5}})} )
I'll kick the ball rolling
EXERCISE 2A
Q5j
Been spending only 3 minutes on this but i got my final answer in radians, not exact value, as required in the question.