Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Please help with these three questions they the only three I couldn't do from the ex (1 Viewer)
- Thread starter kpad5991
- Start date
ichila101
Split arrowhead
Re: Please help with these three questions they the only three I couldn't do from the
Sent from my SM-G900I using Tapatalk
You have already tried finding the indefinite integral for all three of them?
Sent from my SM-G900I using Tapatalk
ichila101
Split arrowhead
Re: Please help with these three questions they the only three I couldn't do from the
Try differentiating the denominator of the first one and tell me whst you get
For the second one think of what you can do to a fraction when the numerator is made up of two different variables that are being added together
For the third one how can you turn the fraction into a reciprocal
Try differentiating the denominator of the first one and tell me whst you get
For the second one think of what you can do to a fraction when the numerator is made up of two different variables that are being added together
For the third one how can you turn the fraction into a reciprocal
Last edited:
ichila101
Split arrowhead
Re: Please help with these three questions they the only three I couldn't do from the
Sent from my SM-G900I using Tapatalk
Yes thats right and what did you get when you substituted (1,1)Is it y=ln (x^2+5x+4) + C
And then you substitute (1,1) to find C. But the solution is y=log (x^2+5x+4/10) +1
Sent from my SM-G900I using Tapatalk
ichila101
Split arrowhead
Re: Please help with these three questions they the only three I couldn't do from the
C shouldnt be equating to 0
You subbed the x=1 in log((1)^2 + 5(1) + 4)?C=0
So y = log (x^2 +5x+4)
But the solution is as mentioned above y= log (x^2+5x+4/10) +1
C shouldnt be equating to 0
Last edited:
ichila101
Split arrowhead
Re: Please help with these three questions they the only three I couldn't do from the
Sent from my SM-G900I using Tapatalk
Did you try turning it into reciprocal and then integrating it?AAah okay I get what I did wrong thanks now I need 9e
Sent from my SM-G900I using Tapatalk
Re: Please help with these three questions they the only three I couldn't do from the
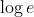 (keeping in mind that logarithms are implicitly in base
(keeping in mind that logarithms are implicitly in base  ).
).
EvaluateOkay I got 9e finally but how is y(e) = e+1!??
I got y= 2+x -log x
So y(e) = 2+e-log e
ichila101
Split arrowhead
Re: Please help with these three questions they the only three I couldn't do from the
Sent from my SM-G900I using Tapatalk
What does loge (e) equate toOkay I got 9e finally but how is y(e) = e+1!??
I got y= 2+x -log x
So y(e) = 2+e-log e
Sent from my SM-G900I using Tapatalk

