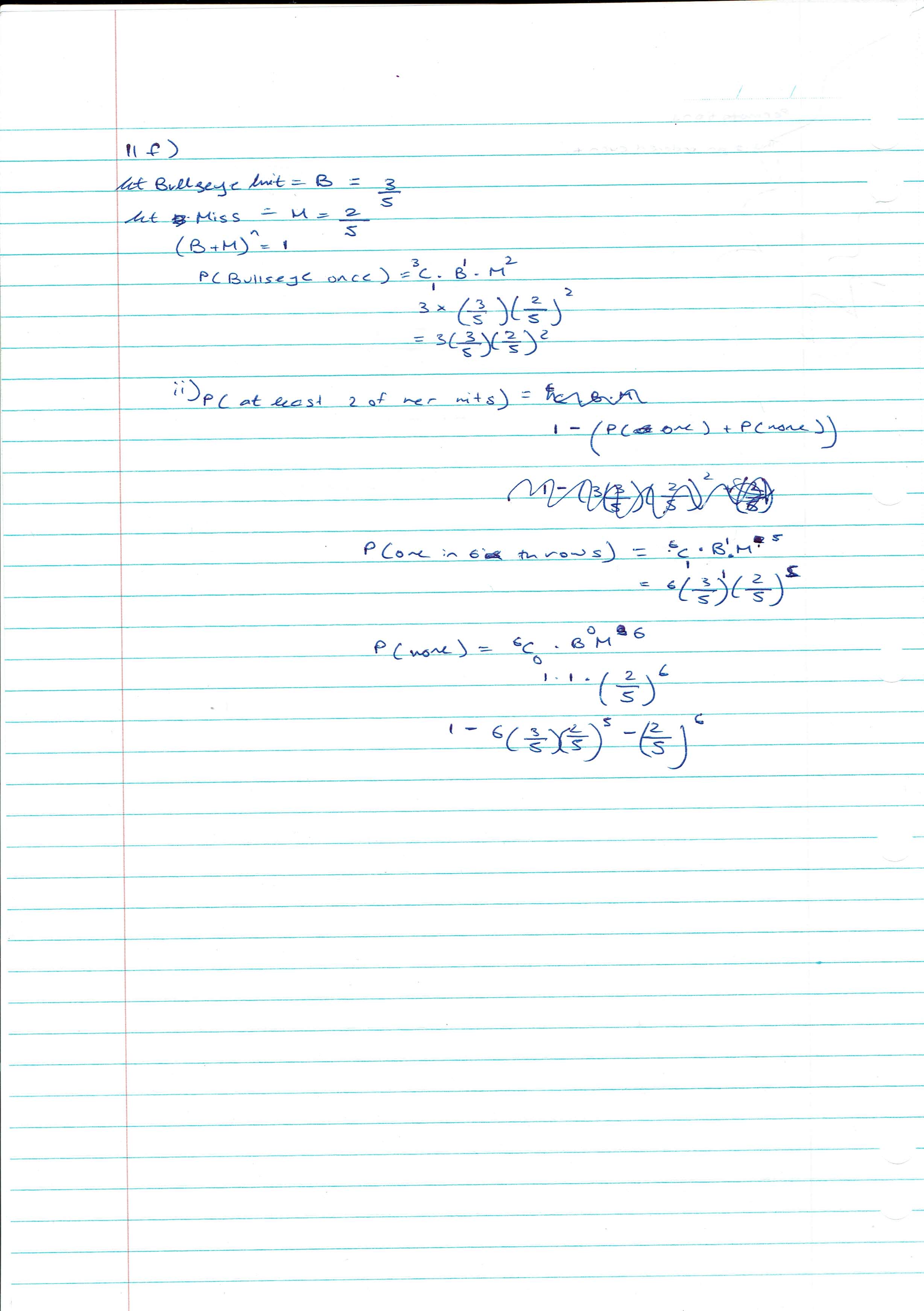Exp
Member
Could someone explain this? I had a look at the answers and don't entirely understand it.. especially part 2.
from 11 f)
A darts player calculates that when she aims for the bullseye the probability of 3/5 her hitting the bullseye is with each throw.
(i) Find the probability that she hits the bullseye with exactly one of her first three throws.
(ii) Find the probability that she hits the bullseye with at least two of her first six throws.
from 11 f)
A darts player calculates that when she aims for the bullseye the probability of 3/5 her hitting the bullseye is with each throw.
(i) Find the probability that she hits the bullseye with exactly one of her first three throws.
(ii) Find the probability that she hits the bullseye with at least two of her first six throws.