Hi I need help with a question as I am getting k as a non-integer when doing the binomial expansion.
Question: Find the term independent of x in the expansion of:
^{14} )
My attempt:
^{14} = \binom{14}{k}(2x^{-4})^{14-k}(x^2)^k)

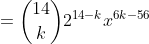
Therefore term independent of x when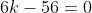
but at this point k = 28/3 and I am not sure how to move forward.
How do I solve this question?
Question: Find the term independent of x in the expansion of:
My attempt:
Therefore term independent of x when
but at this point k = 28/3 and I am not sure how to move forward.
How do I solve this question?
Last edited:
