-
Looking for HSC notes and resources? Check out our Notes & Resources page
HSC 2017 MX2 Integration Marathon (archive) (1 Viewer)
- Thread starter leehuan
- Start date
- Status
- Not open for further replies.
Re: HSC 4U Integration Marathon 2017
Lol i think this method is a complete unintended tedious one
use the substitution x=sqrt(3)sin(theta). the new limits are now 0 to sin^-1(1/sqrt(3)). and dx=sqrt(3)cos(theta). Sub it in, the integrand becomes 9sin^2(theta)cos^2(theta). Which can be written as 9/4(sin2theta)^2. Using the double angle cos formula, it will turn out to be 9/8(1-cos(4theta)). Now integrating it, it becomes 9/8(theta-(sin4theta)/4)) from 0 to sin^-1(1/sqrt3). Expanding out the sin4theta (either by continuous use of double angle formula or DMT) and subbing in the limits will give a final answer of 1/8(9arcsin(1/sqrt3)-sqrt2).
soz for no latex might add it when im free
Lol i think this method is a complete unintended tedious one
use the substitution x=sqrt(3)sin(theta). the new limits are now 0 to sin^-1(1/sqrt(3)). and dx=sqrt(3)cos(theta). Sub it in, the integrand becomes 9sin^2(theta)cos^2(theta). Which can be written as 9/4(sin2theta)^2. Using the double angle cos formula, it will turn out to be 9/8(1-cos(4theta)). Now integrating it, it becomes 9/8(theta-(sin4theta)/4)) from 0 to sin^-1(1/sqrt3). Expanding out the sin4theta (either by continuous use of double angle formula or DMT) and subbing in the limits will give a final answer of 1/8(9arcsin(1/sqrt3)-sqrt2).
soz for no latex might add it when im free
Last edited:
Green Yoda
Hi Φ
- Joined
- Mar 28, 2015
- Messages
- 2,859
- Gender
- Male
- HSC
- 2017
Re: HSC 4U Integration Marathon 2017
It will be a while before I attempt in this marathon...
It will be a while before I attempt in this marathon...
Paradoxica
-insert title here-
Re: HSC 4U Integration Marathon 2017
This isn't funny anymore.
...
This isn't funny anymore.
Paradoxica
-insert title here-
Re: HSC 4U Integration Marathon 2017
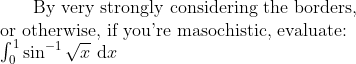
Re: HSC 4U Integration Marathon 2017
Worth exposing 2017'ers to since they may not have followed the older Marathons. (Wasn't intended as a joke integral.)...
This isn't funny anymore.
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,657
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 4U Integration Marathon 2017
If the integrals easy enough to inspect such as a reverse product rule then you can... You can't just do what Paradoxica does and just say for question 16 integral "by inspection...".Quick question with regards to integrals. are we allowed to integrate by inspection in the hsc. thanks
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,657
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 4U Integration Marathon 2017
 Chose otherwise soz. I can see the borders way but why bother...
Chose otherwise soz. I can see the borders way but why bother...
Re: HSC 4U Integration Marathon 2017
<a href="https://www.codecogs.com/eqnedit.php?latex=\int&space;\sqrt{cos2x}/(sinx)&space;dx" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\int&space;\sqrt{cos2x}/(sinx)&space;dx" title="\int \sqrt{cos2x}/(sinx) dx" /></a>
<a href="https://www.codecogs.com/eqnedit.php?latex=\int&space;\sqrt{cos2x}/(sinx)&space;dx" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\int&space;\sqrt{cos2x}/(sinx)&space;dx" title="\int \sqrt{cos2x}/(sinx) dx" /></a>
Re: HSC 4U Integration Marathon 2017
Anyway, just note that by point symmetry, the area under the curve (and hence the integral) is half the area of the rectangle enclosing the arc in question, i.e. 1/2 * (pi/2) = pi/4.
I guess he considered that 'masochistic'? (Not really sure how it is, but anyway.)Chose otherwise soz. I can see the borders why but why bother...
Anyway, just note that by point symmetry, the area under the curve (and hence the integral) is half the area of the rectangle enclosing the arc in question, i.e. 1/2 * (pi/2) = pi/4.
Last edited:
Re: HSC 4U Integration Marathon 2017
aww no using inspection in everything you integrate. thanks anyway drsoccerballIf the integrals easy enough to inspect such as a reverse product rule then you can... You can't just do what Paradoxica does and just say for question 16 integral "by inspection...".
Paradoxica
-insert title here-
Re: HSC 4U Integration Marathon 2017
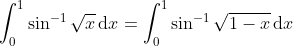
Then use the fact that:
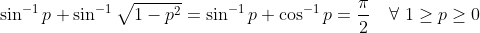
Too long. One can observe:Chose otherwise soz. I can see the borders way but why bother...
Then use the fact that:
Re: HSC 4U Integration Marathon 2017
Exactly. But I guess exposure to some questions could be helpful.At school has anyone started 4 unit integration? Because at my school we don't start it till next year term 2
Paradoxica
-insert title here-
Re: HSC 4U Integration Marathon 2017
^2 -1}}{(2\cos{x})^2 -2} (-\sqrt{2} \sin{x} \text{d}x) \\\\ = \sqrt{2} \int \frac{\sec{\theta} \tan^2{\theta}}{\sec^2{\theta} -2} \text{d}\theta = \sqrt{2} \int \frac{\sin^2{\theta} \cos{\theta} \, \, \text{d}(\theta)}{(1-\sin^2{\theta}) (2\sin^2{\theta}-1)} \\\\ \sin^2{\theta} \equiv (2\sin^2{\theta}-1) + (1-\sin^2{\theta}) \\\\ \Rightarrow \frac{\sin^2{\theta}}{(1-\sin^2{\theta})(2\sin^2{\theta}-1)} \equiv \sec^2{\theta} + \frac{1}{2\sin^2{\theta}-1} \\\\ \sqrt{2}\int \sec{\theta} \, \text{d}\theta - \sqrt{2} \int \frac{\text{d}(\sin{\theta})}{1-2\sin^2{\theta}})
} + \frac{1}{2} \log{\left(\frac{1-\sqrt{2}\sin{\theta}}{1+\sqrt{2}\sin{\theta}} \right)} + \mathcal{C} \\\\ \sec{\theta} = \sqrt{2}\cos{x},\, \tan{\theta} = \sqrt{\cos{2x}}, \sin{\theta} = \frac{\sqrt{\cos{2x}}}{\sqrt{2} \cos{x}} \\\\ \sqrt{2} \log(\sqrt{2}\cos{x} + \sqrt{\cos{2x}}) + \frac{1}{2} \log{\left( \frac{\cos{x} - \sqrt{\cos{2x}}}{\cos{x} + \sqrt{\cos{2x}}} \right)} + \mathcal{C})
Simplifying the derivative in Mathematica confirms the result.
Simplifying the derivative in Mathematica confirms the result.
Re: HSC 4U Integration Marathon 2017
<a href="https://www.codecogs.com/eqnedit.php?latex=\int&space;x(\arctan&space;x)^{2}&space;dx" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\int&space;x(\arctan&space;x)^{2}&space;dx" title="\int x(\arctan x)^{2} dx" /></a>
<a href="https://www.codecogs.com/eqnedit.php?latex=\int&space;x(\arctan&space;x)^{2}&space;dx" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\int&space;x(\arctan&space;x)^{2}&space;dx" title="\int x(\arctan x)^{2} dx" /></a>
Last edited:
- Status
- Not open for further replies.
