-
Looking for HSC notes and resources? Check out our Notes & Resources page
Interesting Induction Question (1 Viewer)
- Thread starter Mahan1
- Start date
Paradoxica
-insert title here-
Hm.
Well I'm not going to induct since I can't see a way to push forward.
But I still have a solution
The statement is trivial for n=1, going from left to right. The reverse direction has a corresponding theorem which I will leave to the interested reader.
For n=2, this corresponds to the Pythagorean Identity, for which there exist infinitely many solutions.
This second statement has the equivalent form:
x² + y² = (m² + n²)², which is obvious from the parametric solution. (look it up if you need to)
Now, suppose n is an odd number times some power of 2.
x² + y² = z2k(2l + 1)
Using the pythagorean solution, this reduces the problem into:
m² + n² = z2k - 1(2l + 1)
Which removes a factor of 2 from the exponent. This can be repeated as many times as necessary until the power of 2 vanishes.
Thus, it is sufficient to consider only the odd cases.
For the equation x² + y² = x2n + 1
The parametric form of the solution is given by:
x = a(a² + b²)2nt + n + 1
y = b(a² + b²)2nt + n + 1
z = (a² + b²)2t + 1
And the statement has solutions for all natural n.
Since we were only interested in the existence of a solution, and not infinitely many or finite solutions, all the statements can be reversed to construct solutions for all exponents.
Well I'm not going to induct since I can't see a way to push forward.
But I still have a solution
The statement is trivial for n=1, going from left to right. The reverse direction has a corresponding theorem which I will leave to the interested reader.
For n=2, this corresponds to the Pythagorean Identity, for which there exist infinitely many solutions.
This second statement has the equivalent form:
x² + y² = (m² + n²)², which is obvious from the parametric solution. (look it up if you need to)
Now, suppose n is an odd number times some power of 2.
x² + y² = z2k(2l + 1)
Using the pythagorean solution, this reduces the problem into:
m² + n² = z2k - 1(2l + 1)
Which removes a factor of 2 from the exponent. This can be repeated as many times as necessary until the power of 2 vanishes.
Thus, it is sufficient to consider only the odd cases.
For the equation x² + y² = x2n + 1
The parametric form of the solution is given by:
x = a(a² + b²)2nt + n + 1
y = b(a² + b²)2nt + n + 1
z = (a² + b²)2t + 1
And the statement has solutions for all natural n.
Since we were only interested in the existence of a solution, and not infinitely many or finite solutions, all the statements can be reversed to construct solutions for all exponents.
Exactly, That is the idea.^{2} + \left(yz^{k}\right)^2 = z^{2k+1}$ as our solution. The idea for even powers $2k$ is similar. Start with a known solution $a^2 + b^2 = c^2$, then multiply both sides by $c^{2k-2}$, so we have the solution $\left(ac^{k-1}\right)^{2} + \left(bc^{k-1}\right)^2 = c^{2k}$.$)
basically you prove it for n=1 and n=2 which is obvious, then we can show if the statement is true for n=k then its true for n=k+2, that's basically what you've done with splitting it into two cases, odd and even.
Paradoxica
-insert title here-
The induction is trivial. The difficult step is proving the non-trivial base case, n=2, which is awfully tedious.Well, I think that question was relatively easy for this forum so I decided to share a slightly more challenging induction question:
prove for every positive integer n, if
for all i = 1,..,n
then
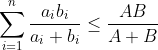
where
Paradoxica
-insert title here-
n=2 is true by Minkowski's Inequality (for Sums)Well, I think that question was relatively easy for this forum so I decided to share a slightly more challenging induction question:
prove for every positive integer n, if
then
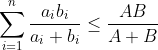
where
The specified case is p=-1, which is applicable since all variables involved are strictly positive.
To be honest that was how I solved it initially but when I tried to solve it without using that inequality, at extension2 level, I also had to go through a not pleasant algebraic manipulation. Just to confirm for n=2 did you multiply the inequality by
Last edited:
Paradoxica
-insert title here-
I didn't even attempt it lolTo be honest that was how I solved it initially but when I tried to solve it without using that inequality, at extension2 level, I also had to go through a not pleasant algebraic manipulation. Just to confirm for n=2 did you multiply the inequality by?
BUT
I have a method.
Jensen's Inequality in 2 variables.
The function f(x,y) → 1/(1/x + 1/y) is convex in x and y, so:
(f(a₁,b₁) + f(a₂,b₂))/2 ≤ f((a₁+a₂)/2,(b₁+b₂)/2)
Multiply both sides by 2 to achieve the desired result.
Last edited:
haha, fair enough. I think if you try that, it's not that bad.
But it's still ugly.
That's a nice method. Jensen's inequality is powerful, it's a shame we don't learn it in 4unit
Paradoxica
-insert title here-
As an added aside, the hessian matrix for the function is zero, so it has no determined convexity.
But the first partial derivatives are strictly negative, so the function is strictly decreasing along the individual axes.
Monotone and decreasing, with limiting slope towards zero, this should be sufficient for convexity. (Unsure if it technically follows)
But the first partial derivatives are strictly negative, so the function is strictly decreasing along the individual axes.
Monotone and decreasing, with limiting slope towards zero, this should be sufficient for convexity. (Unsure if it technically follows)
did you evaluate the Hessian matrix at a particular point? Otherwise I don't know how you got det hessian matrix = 0
Also about having negative first partial derivative in each direction, I haven't done any calculation to check whether is negative or not but I take your word for it. That does not imply the function is monotone or decreasing in every direction moreover the way the function is defined, the boundaries (x,0) and (0,y) are undefined unless you force the function at those boundaries to be zero.
Paradoxica
-insert title here-
The hessian matrix is zero anywhere the function is defined. Check it yourself, it's not that bad.
as for the technical matter, the function is positive for positive inputs, and monotone decreasing by the first derivatives (maybe now would be a good time to start learning vectors lmao) along each respective direction (but not overall decreasing), with interesting behaviour when x and y are very close in magnitude.
Yes you're right I checked the matrix and the determinant is indeed zero. I do agree the function is decreasing in each axis but I think the first partial in each direction is strictly positive.
Paradoxica
-insert title here-
Well that doesn't prevent convexity, which is the desired property...
Needs more investigation.
If f is convex, the inequality should be the other way round.
It is easy to show that function f(x,y) = (xy)/(x+y) (x, y > 0) is not convex (e.g. along the line y = 1, the function is x/(x+1) (x > 0), which is not convex).
To get the inequality direction you wrote, we'd want f(x,y) to be concave, so you should try investigating concavity rather convexity, if you want to try that method.
To get the inequality direction you wrote, we'd want f(x,y) to be concave, so you should try investigating concavity rather convexity, if you want to try that method.
Paradoxica
-insert title here-
Yes, I already realised that mistake...
Concavity is what should have been the focus.
It's trivial to prove concavity along a fixed value of y, var. x and vice versa.
The plane slope vector of the graph is increasing at a decreasing rate, which I think should be sufficient for concavity.