Prove the equation of a line and a circle in complex plane has a general form of :
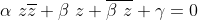
where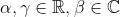
Hence, or otherwise, prove
If are complex numbers
are complex numbers
which satisfies below condition:
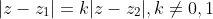
then they are locus of circles in complex plane.
where
Hence, or otherwise, prove
If
which satisfies below condition:
then they are locus of circles in complex plane.
Last edited:

