Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Complex Number questions (1 Viewer)
- Thread starter BenHowe
- Start date
What is w? There won't exist such real a and b if w is real, but if w is non-real, then there will.There might be a couple, but this is the first...
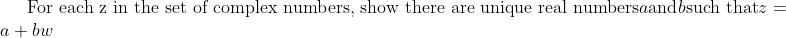
BenHowe
Active Member
- Joined
- Aug 20, 2015
- Messages
- 354
- Gender
- Male
- HSC
- 2016
- Uni Grad
- 2020
There are various ways to show it. It comes out essentially immediately with a bit of Linear Algebra knowledge.
Add the negative of z to both sides and use associativity of addition.I'm also struggling with using field and order axioms to prove stuff like given
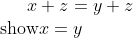
Depends which ones. You can say things like "associativity of addition" etc.How do you like refer to the order/field axioms
Ahh gotcha tbh I worked it out. Thanks for your help. The thing I don't understand still are partial orders and how u'd use it for a q like this. Also what the curved inequality signs mean.
View attachment 33827
There are various ways to show it. It comes out essentially immediately with a bit of Linear Algebra knowledge.



