jjjcjjj892
New Member
- Joined
- Apr 22, 2017
- Messages
- 16
- Gender
- Male
- HSC
- 2018
Can anyone help me integrate sec^3(x) without using the reduction formula?
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Thanks for the reply, the way I progressed was going:I think you can do it this way with IBP:

use the identity tan^2(x) = sec^2(x) - 1Thanks for the reply, the way I progressed was going:
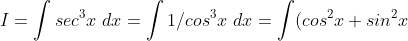/cos^3x \ dx \\ \\ = \int secx \ dx + \int sin^2x/cos^3x \ dx )
And its at this point I get lost, I can get the sec integral fine, its given, but the integralis confusing
Thank you, that made it very clear cheers everyone for the help.

