Suppose we have the integral
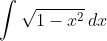
We can make the substitution , which is undoubtedly valid because the range of the substitution
, which is undoubtedly valid because the range of the substitution  is the same as the domain of the integrand
is the same as the domain of the integrand  .
.
But what about an integrand whose domain is all real numbers? For example:
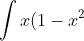\,dx)
Obviously we can integrate this without a substitution to get x^2 - (1/4) x^4) but suppose we wanted to use
but suppose we wanted to use 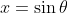 . We would end up with
. We would end up with  x^2 - (1/4) x^4 + 1/4) , which is still correct.
, which is still correct.
But is the substitution valid? Since the range of the substitution is still , which doesn't cover the domain of the integrand
, which doesn't cover the domain of the integrand 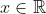 .
.
We can make the substitution
But what about an integrand whose domain is all real numbers? For example:
Obviously we can integrate this without a substitution to get
But is the substitution valid? Since the range of the substitution is still

