Point P, Q are h metres apart in a vertical line. A particle is projected with speed C from P towards Q at the same instant, another is projected with speed C from Q towards P.
If the resistance of the medium is proportional to the speed and the terminal speed is C, show that the particles meet after time
)
provided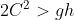 .
.
As per upwards and downwards cases
I could get (if I am right!)
for upwards:
)
\right])
for downwards:
)
\right])
I understand
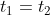
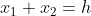
How do I use terminal velocity C to get the result?
Thanks for your help.
If the resistance of the medium is proportional to the speed and the terminal speed is C, show that the particles meet after time
provided
As per upwards and downwards cases
I could get (if I am right!)
for upwards:
for downwards:
I understand
How do I use terminal velocity C to get the result?
Thanks for your help.
