Given that
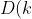 - kD(k-1) = -[D(k-1) - (k-1)D(k-2)] )
for some
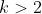
.
Set
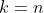
to get
:\, D(n) - nD(n-1) = -[\color{red}{D(n-1) - (n-1)D(n-2)}\color{black}] )
That red expression on the RHS looks very similar to the LHS.
Set
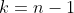
to get
:\, \color{red}{D(n-1) - (n-1)D(n-2)} \color{black}= -[D(n-2) - (n-2)D(n-3)] )
Substitute (2) back into (1) to get:
:\, D(n) - nD(n-1) = -[-[\color{blue}D(n-2) - (n-2)D(n-3)\color{black}]] )
Set
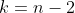
to get
:\, \color{blue}{D(n-2) - (n-2)D(n-3)} \color{black}= -[D(n-3) - (n-3)D(n-4)] )
Substitute (4) back into (3) to get:
:\, D(n) - nD(n-1) = -[-[-[D(n-3) - (n-3)D(n-4)]]] )
If you look at (1), (3) and (5):
:\, D(n) - nD(n-1) = -[{D(n-1) - (n-1)D(n-2)}] )
:\, D(n) - nD(n-1) = -[-[D(n-2) - (n-2)D(n-3)]] )
:\, D(n) - nD(n-1) = -[-[-[D(n-3) - (n-3)D(n-4)]]] )
It's pretty clear what is happening on the RHS.
If you keep repeating this process, then for any finite
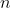
you will eventually get
 - nD(n-1) = -[-[-[...-[D(2) - (2)D(1)]]]] = -[-[-[...-[1]]]])
So how many minus signs are on the RHS? Well let's look at those equations again:
:\, D(n) - nD(n-1) = \color{red}-\color{black}[D(n-\color{red}1\color{black})-...] )
:\, D(n) - nD(n-1)= \color{red}-\color{black}[\color{red}-\color{black}[D(n-\color{red}2\color{black})-...] )
:\,D(n) - nD(n-1)= \color{red}-\color{black}[\color{red}-\color{black}[\color{red}-\color{black}[D(n-\color{red}3\color{black})-...] )
That red number happens to be the same as the number of minus signs on the RHS.
Now
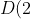 = D(n-(n-2)))
so when we eventually reduce that term on the RHS to
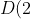 )
then there will be
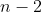
minus signs on the RHS.
That is,
 - nD(n-1) = \underbrace{-[-[-[}_{n-2\,\,\mathrm{times}} ... [1] ]]] = (-1)^{n-2} = (-1)^n \cdot \frac{1}{(-1)^{2}} = (-1)^n)
Note that the LHS contains
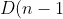 )
and
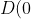 )
is not defined. Therefore we need
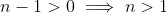
.