Recall that

represents the vector from

to

.
 )
is the angle that this makes with the positive real axis.
Draw an Argand diagram and mark on it the points

and
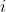
.
Now imagine a variable point

moving around the diagram. We want to find the values of

for which the vectors

and
 )
are parallel and facing the same way.
For the second one we can interpret it as finding all

for which an angle equivalent to
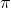
is obtained by subtracting the arguments of the vector
 )
from

.