davidgoes4wce
Well-Known Member
Statistics Marathon & Questions
This is a marathon thread for statistics. Please aim to pitch your questions for first-year/second-year university level statistics. Excelling & gifted/talented secondary school students are also invited to contribute.
This is also a place to discuss university level statistics. For specific subjects or even higher level stuff, this is probably not the best thread. (Feel to create your own in those instances)
(mod edit 7/6/17 by dan964)
===============================

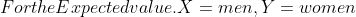
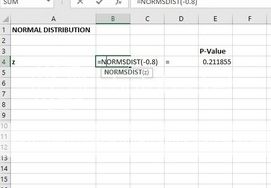
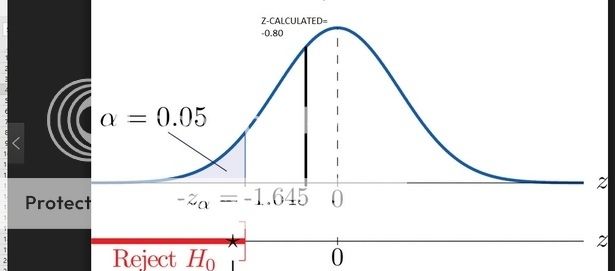
=85, Var(X)=144, E(Y)=68, Var(Y)=64, E(Lift)=500 )
= 4 \times 85 + 68 \times 3 +500 = 1044 )
= 4^{2} Var (X)+ 3^{2} Var (Y) )

This is a marathon thread for statistics. Please aim to pitch your questions for first-year/second-year university level statistics. Excelling & gifted/talented secondary school students are also invited to contribute.
This is also a place to discuss university level statistics. For specific subjects or even higher level stuff, this is probably not the best thread. (Feel to create your own in those instances)
(mod edit 7/6/17 by dan964)
===============================
Last edited by a moderator: