Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
ACST212 - Combinatorial Probability (2 Viewers)
- Thread starter BenHowe
- Start date
Try and consider the die modulo 3.Hey need some help with questions. Here's the 1st one.
View attachment 34229
Edit I'd like a hint not the answer. Thanks heaps
BenHowe
Active Member
- Joined
- Aug 20, 2015
- Messages
- 354
- Gender
- Male
- HSC
- 2016
- Uni Grad
- 2020
Edit: I was wrong xD
Hey here's the rest of the q and I managed to do b) but my expression with c inst quite working.
and I managed to do b) but my expression with c inst quite working.
I get
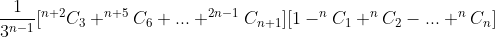
Although I know I should be able to show the answer is always 1/3 because say for the k-1 th roll (k is a positive finite integer) you can think about S mod 3 (where S is the sum of the previous remainders) and it will either be 0,1,2. For each of these outcomes there are exactly 2 corresponding numbers that can be rolled and hence k mod n will be 0. So it will be 2/6=1/3
Hey here's the rest of the q
 and I managed to do b) but my expression with c inst quite working.
and I managed to do b) but my expression with c inst quite working. I get
Although I know I should be able to show the answer is always 1/3 because say for the k-1 th roll (k is a positive finite integer) you can think about S mod 3 (where S is the sum of the previous remainders) and it will either be 0,1,2. For each of these outcomes there are exactly 2 corresponding numbers that can be rolled and hence k mod n will be 0. So it will be 2/6=1/3
They're equally likely by symmetry.Dw I actually got it this time.
Here's the next question
View attachment 34237
I've done a,b and some of c but I'm struggling to show the cases are equally likely. any hints?
Bartimaeus
New Member
- Joined
- Jun 1, 2015
- Messages
- 3
- Gender
- Male
- HSC
- 2016
Hi I have a coupon collector problem, but instead of the expected number of attempts to get all the different coupons, what's the expected number of a particular coupon in satisfying the above constraint?
The actual questions is:
There is an urn with a large number of blue and red balls, what is the expected number of blue balls such that we must have at least 1 blue and 1 red ball ?
The actual questions is:
There is an urn with a large number of blue and red balls, what is the expected number of blue balls such that we must have at least 1 blue and 1 red ball ?
It's half the answer to the usual coupon collector problem (which is to find the expected number of draws to get at least one of every coupon).Hi I have a coupon collector problem, but instead of the expected number of attempts to get all the different coupons, what's the expected number of a particular coupon in satisfying the above constraint?
The actual questions is:
There is an urn with a large number of blue and red balls, what is the expected number of blue balls such that we must have at least 1 blue and 1 red ball ?
In general, it'd be 1/K times the answer to the usual problem, where K is the no. of colours (coupons) available.
Bartimaeus
New Member
- Joined
- Jun 1, 2015
- Messages
- 3
- Gender
- Male
- HSC
- 2016
Thanks heaps for the response. What is the best way of showing this? Like conditional expectation theorem? I'm just wondering because I need to be able to clearly show correct working for q's such as this in the exam.
I can do it by symmetry luike youve said above, but yeah I need to be able to do by as many methods as possible
I can do it by symmetry luike youve said above, but yeah I need to be able to do by as many methods as possible
Last edited:
Probably best to use symmetry. Don't need to use conditional expectation. But for the particular question you asked (with blue and red balls), it's also easy to do it by conditioning on the first draw's colour, and noting the number of draws to get the remaining colour after that is just Geometrically distributed.Thanks heaps for the response. What is the best way of showing this? Like conditional expectation theorem? I'm just wondering because I need to be able to clearly show correct working for q's such as this in the exam.
I can do it by symmetry luike youve said above, but yeah I need to be able to do by as many methods as possible
Bartimaeus
New Member
- Joined
- Jun 1, 2015
- Messages
- 3
- Gender
- Male
- HSC
- 2016
So you would proceed as :
Let R be the random variable denoting the number of red balls selected
Let R1 be the event, the first ball selected is red
Let B1 be the event, the first ball selected is blue
E(R)=P(R1)E(R+1|R1)+P(B1)E(R|B1), by the Conditional Expectation Theorem
Now consider E(R+1|R1), we have obtained 1 red ball. So we will continue to select balls until we have obtained 1 blue ball. So R+1 is a geometric random variable with parameter 1/2. So E(R+1|R1)=2.
Now consider E(R|B1), we have obtained 1 blue ball. We only need 1 red ball. So E(R|B1)=1
Thus E(R)=1/2 X [2] +1/2 X [1]
=3/2 as required
Let R be the random variable denoting the number of red balls selected
Let R1 be the event, the first ball selected is red
Let B1 be the event, the first ball selected is blue
E(R)=P(R1)E(R+1|R1)+P(B1)E(R|B1), by the Conditional Expectation Theorem
Now consider E(R+1|R1), we have obtained 1 red ball. So we will continue to select balls until we have obtained 1 blue ball. So R+1 is a geometric random variable with parameter 1/2. So E(R+1|R1)=2.
Now consider E(R|B1), we have obtained 1 blue ball. We only need 1 red ball. So E(R|B1)=1
Thus E(R)=1/2 X [2] +1/2 X [1]
=3/2 as required



