In exponentiation, we are told that raising something to an integral power (n, say) means multiplying it with itself a total of n times, if n is non-negative. And we also learn fairly early on that should the exponent be negative, then
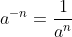
.
We even extend this to the rational field, where with
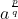
, we are led to believe that there is a unique number

, such that
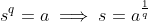
, and we can hence define
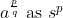
.
But what does it mean to have an irrational power? Clearly
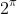
is not 2 multiplied by itself pi times...
Similarly, what does it mean to have an complex power, such as
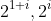
, and is there an explicit formula for calculating such numbers?
My thoughts
Going with my example, since we can approximate pi with rational numbers, e.g. 3.14, 3.14159, etc, I intuitively feel that it approaches a certain limit as we approach ever more accurate approximations of
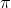
- do we take that limit to be
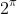
?
Regarding imaginary exponents, I have heard of Euler's formula,
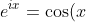 +i\sin (x))
. Do we use this in calculating numbers with complex exponents?
e.g.
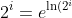}=e^{i\ln (2)}= \cos(\ln(2))+ i\sin(\ln (2)))
?
However, what does it
mean to raise something to a complex power, and do the rules of exponentiation and logarithms still apply when dealing with them?
Breaking a bos hiatus to answer a question I always found interesting in high school.
Your intuition is close with real exponentiation.
First we assume
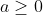
.
If
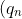)
is a sequence of rationals tending to
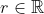
, then we can define
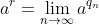
. A little bit of work can show that this is independent of our choice of approximating sequence, and is hence well-defined. (But note that this only gives one answer, a positive real one. We already know that positive numbers have two (1/2)-th powers for instance, so it is clear that this definition is not completely satisfactory...although it is fine if we just want to raise positive reals to positive real powers and get a positive real output.)
If
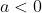
, things aren't so simple even for rational powers because we necessarily enter the complex field by taking roots. One can talk about "principal n-th roots", but this view is ultimately a bit limiting. It is somewhat arbitrary to consider i THE square root of -1, given that (-i)^2 is also -1. (It also means that identities like
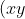^q =x^qy^q)
will not longer be true!) Think carefully about the difference between this situation and the familiar situation of taking the positive square root of a positive number.
For this reason, it is better to just incorporate negative a into our general notion of a complex power.
If z and w are complex and z is nonzero, then we define:
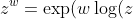)=\exp(w(\log|z|+i\arg(z))).)
Here
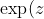=\sum_{k=0}^\infty \frac{z^k}{k!})
is the complex exponential function which converges everywhere, and is equal to
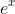
on the real line. Euler's formula and some basic manipulations tell us that
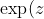=\exp(x+2\pi i))
, which is crucial.
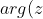)
is the argument of z. Note that arg is a multi-valued function, taking values differing by
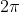
. This is why it is possible for a number to have multiple roots for example.
This multi-valued definition of complex exponentiation is the usual one, and satisfies all the properties one could hope for. (Replacing equality of numbers with equality of sets where appropriate.)
Eg
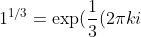)=0,\exp(2\pi i/3),\exp(4\pi i/3))
These are the only distinct values for the expression as k ranges over the integers, because of the
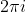
-periodicity of
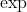
. But Euler's formula also tells us that these are just the complex cube roots of unity, as we might hope. In fact, it should be clear that ANY rational w will result in only finitely many values, no matter what complex value z takes. This agrees with how we would compute such things using "mod-arg form" in MX2.
We can get far more bizarre results though. Notably, z^w generally takes infinitely many values.
Eg2
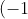^\pi=\exp(\pi\log(-1))=\exp(i\pi^2(2k+1))=\cos(\pi^2(2k+1))+i\sin(\pi^2(2k+1)))
for any integer k.
Or one of my personal favourites
Eg3
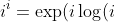)=\exp(i^2(\pi/2+2\pi k))=e^{-\pi(1+4k)/2})
for any integer k, which means that this quantity is real!
It shouldn't bother you too much that it is not easy to think of what it means to do these things. As maths gets built up higher and more abstract it becomes harder to directly connect it to basic concepts and human intuition. Even the notion of a real number itself is a highly abstract concept, the details of which are completely swept under the carpet in high school.
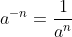 .
. 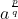 , we are led to believe that there is a unique number
, we are led to believe that there is a unique number  , such that
, such that 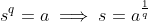 , and we can hence define
, and we can hence define 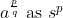 .
.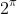 is not 2 multiplied by itself pi times...
is not 2 multiplied by itself pi times... 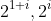 , and is there an explicit formula for calculating such numbers?
, and is there an explicit formula for calculating such numbers? 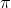 - do we take that limit to be
- do we take that limit to be 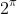 ?
?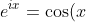 +i\sin (x)) . Do we use this in calculating numbers with complex exponents?
. Do we use this in calculating numbers with complex exponents? 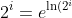}=e^{i\ln (2)}= \cos(\ln(2))+ i\sin(\ln (2))) ?
? 