pencilspanker
Member
- Joined
- Nov 24, 2016
- Messages
- 37
- Gender
- Male
- HSC
- 2019
Hey guys im struggling with a few concepts on complex numbers and just wondering if anyone could clear them up because im legit abt to neck. I know a lot of basic facts but I don't fully understand how they work which is really bugging me... Ok so, for the question:
i)
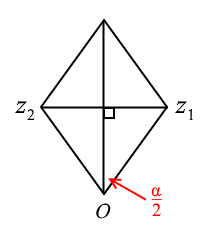
I get that you go arg(z1-z2) - arg (z1+z2) =90o
But what im struggling to understand is why the angle in between those two diagonals in that parallelogram is going to be 90. Like im trying to manipulate the angles that are forming with the positive x axis but i just dont get it...
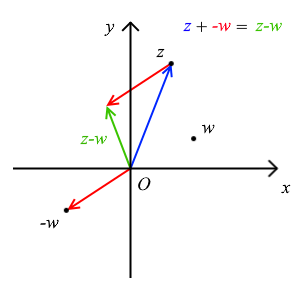
ii) Why can we just randomly say that the vector in the form z - (+z0) will always be the vector running from z0 to z?
iii) If i have the vector --> OC = z, is the vector ---> CO = -z???? And if this is true, how does this work because isnt it that when you put a negative out the front you are multiplying by i2 which means you rotate it by 180o. And if that is true do we call that 180 rotation the position vector whilst the vector ---> CO is just the free vector with the exact same magnitude and direction? Here is a retarded diagram to explain exactly what I mean.
iv) help with this q plsss
THANK U VERY MUCH TO ANYONE THAT HELPS I REALLLLY FREAKING APPRECIATE IT!!!
i)

I get that you go arg(z1-z2) - arg (z1+z2) =90o
But what im struggling to understand is why the angle in between those two diagonals in that parallelogram is going to be 90. Like im trying to manipulate the angles that are forming with the positive x axis but i just dont get it...
ii) Why can we just randomly say that the vector in the form z - (+z0) will always be the vector running from z0 to z?
iii) If i have the vector --> OC = z, is the vector ---> CO = -z???? And if this is true, how does this work because isnt it that when you put a negative out the front you are multiplying by i2 which means you rotate it by 180o. And if that is true do we call that 180 rotation the position vector whilst the vector ---> CO is just the free vector with the exact same magnitude and direction? Here is a retarded diagram to explain exactly what I mean.

iv) help with this q plsss

THANK U VERY MUCH TO ANYONE THAT HELPS I REALLLLY FREAKING APPRECIATE IT!!!