stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
I made a typo in Wolfram earlier. It does give a nice answer.
e^x}{x^2+e^{2x}})
Last edited:
LetNot sure why Wolfram can't give a nice answer.
e^x}{x^2+e^{2x}})
how come a medical student like yourself still has so much interest in math after finishing HSC?Let:
Notice thatis the derivative of
and hence the integral is in the form:
. Thus,
(using the well-known identity
)
once u learn math properly u never forget.how come a medical student like yourself still has so much interest in math after finishing HSC?
Interesting... integration calculator doesn'tI made a typo in Wolfram earlier. It does give a nice answer.
e^x}{x^2+e^{2x}})
I have a feeling @vernburn likes maths more than the stuff he is going to do in med.how come a medical student like yourself still has so much interest in math after finishing HSC?
You should attend the integration bee that's being held at UNSW lolThe ultimate tedious integral:
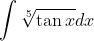
It does look like it doesn’t it! JkjkI have a feeling @vernburn likes maths more than the stuff he is going to do in med.
I may be bored but not enough to attempt this monster!The ultimate tedious integral:
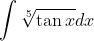
Doesn't look like you were bored of maths considering you got a 99 for 4U. There had to be some interest there lolIt does look like it doesn’t it! Jkjk
In reality, I really only like integration now because there is a certain elegance to it and skill required (and it’s still fresh in my head). I find the rest of maths quite boring and stale imho. My attempts at the above integrals are really just due to boredom (not long till uni starts now though).
This can easily be converted to a much more recognisable integral with the substitution:The ultimate tedious integral:
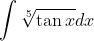
Is the question here to prove this result - i.e. that the integral is 1 irrespective of the value of k - or is this an equation that needs to be solved to find the value(s) of k?I wrote this in the past but I have now forgotten how to solve it.
\left(16^{1-\sqrt{x}}+k\cdot4^{1-\sqrt{x}}+4\right)}{\left(4^{\sqrt{x}}+k\cdot2^{\sqrt{x}}+4\right)\left(4^{1-\sqrt{x}}+k\cdot2^{1-\sqrt{x}}+4\right)}\right)dx=1)
The integral is 1 irrespective of the value of k.Is the question here to prove this result - i.e. that the integral is 1 irrespective of the value of k - or is this an equation that needs to be solved to find the value(s) of k?
can you post the solution here? This gives me a headache for the last few daysI wrote this in the past but I have now forgotten how to solve it.
Edit: I remember how to solve it now.
Yeah lol, some factoring trick I imagine, or King Rule but I dont see how that is used.can you post the solution here? This gives me a headache for the last few days
What tricks have you tried?can you post the solution here? This gives me a headache for the last few days
I've tried all the techniques above. I think the problem will be solved by substituting x with another variable t and we got I + I = 2 so I = 1.What tricks have you tried?
The following techniques are NOT required.
integration by parts
differentiation under the integral sign
hyperbolic function
