Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
First Year Mathematics A (Differentiation & Linear Algebra) (1 Viewer)
- Thread starter Flop21
- Start date
Flop21
Well-Known Member
- Joined
- May 12, 2013
- Messages
- 2,802
- Gender
- Female
- HSC
- 2015
Re: MATH1131 help thread
I'm watching Kahn academy videos on vectors. I'm understanding everything so far, the guy is using (x,y) notation, but then suddenly switches to a different notation I'm not familiar with. This happened in my class lecture as well.
Can someone help me understand what this notation means:

I'm watching Kahn academy videos on vectors. I'm understanding everything so far, the guy is using (x,y) notation, but then suddenly switches to a different notation I'm not familiar with. This happened in my class lecture as well.
Can someone help me understand what this notation means:

soloooooo
Well-Known Member
- Joined
- Feb 13, 2012
- Messages
- 3,310
- Gender
- Female
- HSC
- N/A
Re: MATH1131 help thread
Good idea - perhaps this thread should be moved to the UNSW science faculty sub forum though?
http://community.boredofstudies.org/139/faculties-science-medicine/
Good idea - perhaps this thread should be moved to the UNSW science faculty sub forum though?
http://community.boredofstudies.org/139/faculties-science-medicine/
Flop21
Well-Known Member
- Joined
- May 12, 2013
- Messages
- 2,802
- Gender
- Female
- HSC
- 2015
Re: MATH1131 help thread
Yeah wasn't sure whether to or not. I'm not sure how 1st year uni maths differs from uni to uni, but assumed it would be similar. So everyone can just post their math problems and get help here [or mods can move it wherever best].Good idea - perhaps this thread should be moved to the UNSW science faculty sub forum though?
http://community.boredofstudies.org/139/faculties-science-medicine/
Re: MATH1131 help thread
. $\mathbb{R}^2$ refers to the set of all ordered pairs of real numbers (think of the Cartesian plane).$)
How is R^2 different to R? (and by R I mean the special R/real numbers).
Re: MATH1131 help thread

I'm watching Kahn academy videos on vectors. I'm understanding everything so far, the guy is using (x,y) notation, but then suddenly switches to a different notation I'm not familiar with. This happened in my class lecture as well.
Can someone help me understand what this notation means:

Shadowdude
Cult of Personality
- Joined
- Sep 19, 2009
- Messages
- 12,141
- Gender
- Male
- HSC
- 2010
Re: MATH1131 help thread
the unsw mathematics society has a facebook page for such queries
Did you join MathSoc?
the unsw mathematics society has a facebook page for such queries
Did you join MathSoc?
dan964
what
Re: MATH1131 help thread
(edit: Integrand already answered this)
That notation with a vertical arrow is used to refer to a vector. Typically, e.g. in MATH201 at UOW, this notation is used to refer to row vectors; although it can be used to refer to column vectors as in the case here.I'm watching Kahn academy videos on vectors. I'm understanding everything so far, the guy is using (x,y) notation, but then suddenly switches to a different notation I'm not familiar with. This happened in my class lecture as well.
Can someone help me understand what this notation means:

(edit: Integrand already answered this)
Last edited:
Silly Sausage
Well-Known Member
- Joined
- Dec 8, 2014
- Messages
- 594
- Gender
- Male
- HSC
- 2014
Re: MATH1131 help thread
Some of the math tutors\lecturers at USYD refer to the arrow notation as the "Russian way" of writing it. Apparently the normal westernised one is basically a squiggly line that's under the letter.
That notation with a vertical arrow is used to refer to a vector. Typically, e.g. in MATH201 at UOW, this notation is used to refer to row vectors; although it can be used to refer to column vectors as in the case here.
(edit: Integrand already answered this)
Some of the math tutors\lecturers at USYD refer to the arrow notation as the "Russian way" of writing it. Apparently the normal westernised one is basically a squiggly line that's under the letter.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Re: MATH1131 help thread
If you got given a vector as defined by ray AB though or something, then well you need the arrow above no matter what.
I guess that's just for the vector a etc.Some of the math tutors\lecturers at USYD refer to the arrow notation as the "Russian way" of writing it. Apparently the normal westernised one is basically a squiggly line that's under the letter.
If you got given a vector as defined by ray AB though or something, then well you need the arrow above no matter what.
Paradoxica
-insert title here-
Re: MATH1131 help thread
I write with a half-arrow.
I write with a half-arrow.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Re: MATH1131 help thread
Oh that, so do I. Who the hell has the time to put in the complete > when you can just use \I write with a half-arrow.
Paradoxica
-insert title here-
Re: MATH1131 help thread
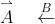
This is for your sake, and possibly mine if I ever have to use vectors on BOS.
Lol, an italicised backward slash is a vertical line. This is amusing.
Oh that, so do I. Who the hell has the time to put in the complete > when you can just use \
Code:
\overset{\rightharpoonup }{A} \quad \overset{B}{\leftarrow}This is for your sake, and possibly mine if I ever have to use vectors on BOS.
Lol, an italicised backward slash is a vertical line. This is amusing.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Re: MATH1131 help thread
Ah thanks. If I forget I'll just consult daum though. I've only recently begun typing LaTeX myself without any other software
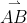
I use a swiggly line under stuff like b but when I refer to a vector with labelled endpoints I do that
Ah thanks. If I forget I'll just consult daum though. I've only recently begun typing LaTeX myself without any other software
I use a swiggly line under stuff like b but when I refer to a vector with labelled endpoints I do that
Re: MATH1131 help thread
$ (so it depends on $\varepsilon$) such that if $x>M$, then $|f(x)-L|<\varepsilon$.$)
How do I do the last parts of these questions. I understand the rest, but have no idea what to do when it comes to throwing in epsilon in there (the last questions/s).

Shadowdude
Cult of Personality
- Joined
- Sep 19, 2009
- Messages
- 12,141
- Gender
- Male
- HSC
- 2010
Re: MATH1131 help thread
i hear he's pretty awesome
i think you should ask the maple consultant that's on tomorrow morningHow do I do the last parts of these questions. I understand the rest, but have no idea what to do when it comes to throwing in epsilon in there (the last questions/s).

i hear he's pretty awesome
Flop21
Well-Known Member
- Joined
- May 12, 2013
- Messages
- 2,802
- Gender
- Female
- HSC
- 2015
Re: MATH1131 help thread
are they suppose to help with actual questions or just how to use maple?i think you should ask the maple consultant that's on tomorrow morning
i hear he's pretty awesome

