leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Is there a higher dimensional implicit differentiation hax (sorry I'm doing maths whilst being a bit hyper) to get me a shortcut for this question
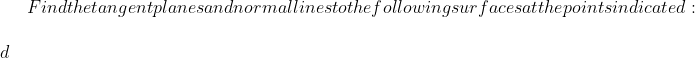 $x^2+y^2+z^2=3$ at the point $(1,1,1))
Or should I just chain rule it because z = +'ve sqrt(...)
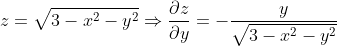
Or should I just chain rule it because z = +'ve sqrt(...)
Last edited by a moderator:

