-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Mathematical Induction - divisibility (1 Viewer)
- Thread starter j1mmy_
- Start date
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
5.5^k + 22. 11^k = 15M + 12 .11^k = 3(5M + 4.11^k) = 3Q
RivalryofTroll
Sleep Deprived Entity
- Joined
- Feb 10, 2011
- Messages
- 3,804
- Gender
- Male
- HSC
- 2013
- Uni Grad
- 2019
5^k = 3M - 2(11)^k [from step 2]
^{n})
I am stuck of step 3.
Here's what I've done so far.
Step 1: Prove true for n = 1
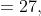
Step 2: Assume n = k
^{k} )
Step 3: Prove true for n = k+1
and now I'm stuck after this.
So continuing....
= 5(3M - 2(11)^k) + (22.(11)^k)
= 15M - 10(11)^k + 22(11)^k
= 15M + 12(11)^k
= 3(5M + 4(11)^k)
= 3Q (Where Q is an integer)
Thus, true for n=k+1
Are we allowed to stop at (1), or do we have to do (2). "Q" is pretty much letting it to be the stuff in the brackets right? (ie. 5M + 4(11)^k)= 3(5M + 4(11)^k) ...(1)
= 3Q (Where Q is an integer) ...(2)
RivalryofTroll
Sleep Deprived Entity
- Joined
- Feb 10, 2011
- Messages
- 3,804
- Gender
- Male
- HSC
- 2013
- Uni Grad
- 2019
Yeah i guess you can stop at (1) and say, which is divisible by 3.Are we allowed to stop at (1), or do we have to do (2). "Q" is pretty much letting it to be the stuff in the brackets right? (ie. 5M + 4(11)^k)
Yeah Q is just an integer.
Alright thanks!Yeah i guess you can stop at (1) and say, which is divisible by 3.
Yeah Q is just an integer.
