-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
integration help (1 Viewer)
- Thread starter Halo189
- Start date
1)1) find the exact area bounded by the parabola y=x^2 and the line y=4-x
2) find the volume of the solid formed when the curve y=(x+5)^2 is rotated about the y-axis from y=1 and y=4

Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
You can find the answer to the 1st question by integrating from -2 to 4 directly in one integral, as the top and bottom curves are the same over that domain =)1)
these are composite areas, so split it up and find pts if intersection
find area:

integrated you get
[4x - x^2/2 - x^3/3]
sub in values
[4(2)-(2)^2/2 -(2)^3/3]-0 + [0- (4(-2)-(-2)^2/2-(-2)^3/3]
=10/3 + 26/3
=36/3 =12
getting to 2)
You'd only need to split it into two integrals if the curves change.
oh yeah trueYou can find the answer to the 1st question by integrating from -2 to 4 directly in one integral, as the top and bottom curves are the same over that domain =)
You'd only need to split it into two integrals if the curves change.
Does the answer still work?

Hang on, I got this
wait, why did carrot leave
Last edited:
integrated is [4x-x^2/2 -x^3/3] then sub in values?The limits of the integral shouldn't be -2 and 2.
The limits should be where 4 – x = x2, which is when.
but yeah I lost the plot
Yeah it's just a bit tedious.integrated is [4x-x^2/2 -x^3/3] then sub in values?
but yeah I lost the plot
then evaluate
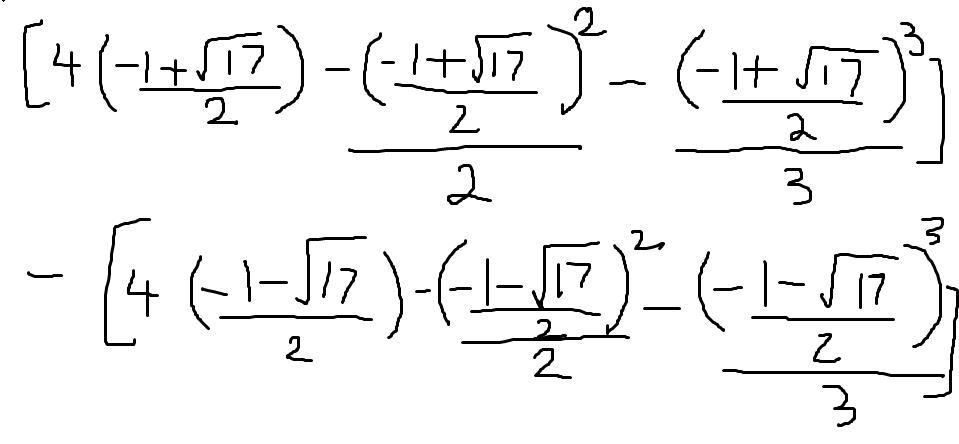
I keep getting it wrong though
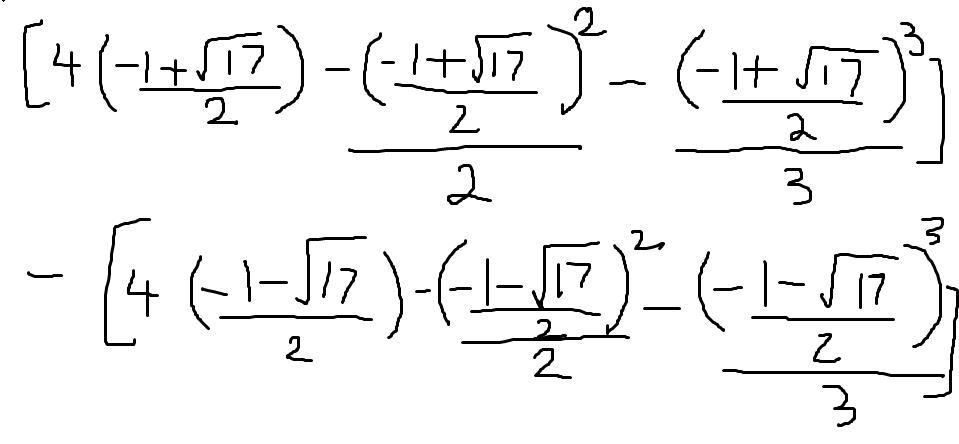
I keep getting it wrong though
Silly Sausage
Well-Known Member
- Joined
- Dec 8, 2014
- Messages
- 594
- Gender
- Male
- HSC
- 2014
The integral should be:

there is no easier way is there?Did you expand the squares and cubes correctly? (The formula to expand cubes is.)
------------------------------------------------
Q2.
y=(x-5)^2
rearrange to make x the subject
√y = x+5
x=√y -5
vol= pi ∫( √y - 5)^2 dy
integrated:
pi[y^2/2 - 5y^3/2 + 25y]
then sub in values
|
|
|
v
scroll down to the answer
Last edited:
yeah very :/Dont worry everyone, I understood it, but the working out to long
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Those limits are yuck.
would they make us do a q like this in an exam. If so, how many marks worth?Those limits are yuck.
=)Thanks for your help
btw, is the answer to q2 correct?
85pi units^3
I dont think so because its way too longwould they make us do a q like this in an exam. If so, how many marks worth?
=)
btw, is the answer to q2 correct?
85pi units^3
And that question is also confusing... answer is apparently 215pi/6
Its fine my friends and I are working on this exercise tomorrow
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
The type of Q (finding the area of the region bounded by a curve and a line) has been done MANY times in examinations!would they make us do a q like this in an exam. If so, how many marks worth?
=)
btw, is the answer to q2 correct?
85pi units^3
But the ugly limits... rarely the case. You will usually have nice limits =)
If the question was just "Find the area of ....", then it would have to be worth 3 marks, possibly 4 if they are generous. One for finding the intersections, one for obtaining the correct integral and one for obtaining the correct answer.
Silly Sausage
Well-Known Member
- Joined
- Dec 8, 2014
- Messages
- 594
- Gender
- Male
- HSC
- 2014

