-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
HSC 2016 MX2 Marathon ADVANCED (archive) (2 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon - Advanced Level
Shouldn't you also assume that the quadratic is one of the factors of an arbitrary polynomial?
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon - Advanced Level
I guess soShouldn't you also assume that the quadratic is one of the factors of an arbitrary polynomial?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon - Advanced Level
How does this allow us to prove that P(p + sqrt(q)) = 0 -> P(p - sqrt(q)) = 0? (for any integer polynomials P)
What do you mean by "both equations are equal"?
How does this allow us to prove that P(p + sqrt(q)) = 0 -> P(p - sqrt(q)) = 0? (for any integer polynomials P)
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2016 4U Marathon - Advanced Level
Well I found the equations that satisfied each root separately and they happened to be equal and thus have the equation has both roots given.What do you mean by "both equations are equal"?
How does this allow us to prove that P(p + sqrt(q)) = 0 -> P(p - sqrt(q)) = 0? (for any integer polynomials P)
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon - Advanced Level
I'm still not sure what you are trying to say here, the equations(x- (p+\sqrt(q)) = 0 ) and
and 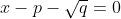 both have a root in common, but why does tha tell us anything special about those equations?
both have a root in common, but why does tha tell us anything special about those equations?
Your argument needs to be clearer for it to be a mathematical proofWell I found the equations that satisfied each root separately and they happened to be equal and thus have the equation has both roots given.
I'm still not sure what you are trying to say here, the equations
Re: HSC 2016 4U Marathon - Advanced Level

Your argument needs to be clearer for it to be a mathematical proof
I'm still not sure what you are trying to say here, the equationsand
both have a root in common, but why does tha tell us anything special about those equations?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon - Advanced Level
Right, then the next step is to show that any integer polynomial P has to have the same property
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon - Advanced Level
This question requires clarification before I can work on it.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon - Advanced Level

This question requires clarification before I can work on it.

Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon - Advanced Level
magnitude of force? speed of ball? I'm not sure how to work with a dimensionless vector.
Re: HSC 2016 4U Marathon - Advanced Level
I think it essentially can have any speed and the answer is not impacted, because the path traced out is the same (I think we are assuming a perfect mathematical universe with no friction or loss of energy in any way, and perfect reflection off the walls; so the ball moves for an infinite amount of time (and the speed is constant)).magnitude of force? speed of ball? I'm not sure how to work with a dimensionless vector.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: HSC 2016 4U Marathon - Advanced Level

 = ( x - (p + \sqrt{q}))(x - (p - \sqrt{q})) = (x-p)^2 - q )
 \ $also has root$ \ p - \sqrt{q} )
 \ $by$ \ f(x) \ $and by the factor theorem$ )
 = f(x) Q(x) + (Ax + B) )
 \ $is a polynomial with rational co-efficients$ )
 - f(x)Q(x) \ $would be a polynomial with irrational co-efficients, which is impossible as$ \ P,Q,f \ $are all polynomials with rational co-efficients$ )
 = f(p + \sqrt{q}) Q(p + \sqrt{q}) + A(p + \sqrt{q}) + B )
 = f(p + \sqrt{q}) = 0 )
 + \sqrt{q} (A) )
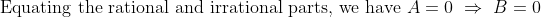
 = f(x) Q(x) )
 = f(p - \sqrt{q}) Q(p - \sqrt{q}) = 0 )

------
(ii) is very similar, where the other solutions are
\sqrt[3]{\beta} )
\sqrt[3]{\beta} )
------
(ii) is very similar, where the other solutions are
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon - Advanced Level
This does not match the answer I got for the special case theta = pi/4I got cos(theta) over 2
Paradoxica
-insert title here-
Re: HSC 2016 4U Marathon - Advanced Level
I am flummoxed. Solutions?
- Status
- Not open for further replies.

