dan964
what
Hi all,
I've posted more detailed markers notes for Q12 and Q14, and a set of solutions (not the official ones but ones I used heavily to mark with, so they may at times differ as they are based on the original set of questions (although I have since adjusted Q12(c), but I have cross checked against the official ones to make sure that they are correct but I may have made a latex error knowing me)
I will still have the question papers until the end of the week so if you want specific feedback send me a DM.
Q12: https://community.boredofstudies.or...mx2-trials-q12-solutions-markers-notes.20036/
Q14: https://community.boredofstudies.or...mx2-trials-q14-solutions-markers-notes.20037/
Some additional general comments/pointers:
Q12 (a) - Some students used a method more complicated then what was needed. Remember that for something to be even, you only need to show that it is or is not a multiple of 2M (where M is any choice of integer). If you did use cases and proof by contradiction for each, you needed to cover all cases even if it was just a cursory statement using W.L.O.G or similarly.
Q12 (b) - Students struggled with this question, expanding and then simplifying was the easiest approach and it was a test of patience and algebra skills. Main tip for this one, is to rework the formula to use the information given (in this case it could be used twice). Also check your solutions are valid (in fact only one student managed to get 2 marks, so close but forgot to eliminate spurious solutions that caused the cosec function to be undefined), its helpful to specify the range for variables in the question e.g.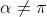 etc.
etc.
Q12 (c) - Many people used the projection formula, to derive the result in part (i), but neglected to explain why they are using the formula (you did not need to use it for part (iii)). Diagrams were also helpful. In part (ii), students often had statements about the shortest distance that were insufficient to show that it was parallel (easiest way was to argue that they shared the same normal implied by an appropriate choice of the (x,y,z) vector, and comment on that the normal was orthogonal (perpendicular) for any choice of normal)
Q12 (d) - Generally this question was done well by all students. But when you setup IBP, don't use the DI table notation (with +/- as rows) that some students had employed as it is non standard notation and not very coherent. With the recursion in part (ii), make sure to evaluate the last term correctly (some students did not or did not show where the recursion ended).
Q14 (a) - Most students did part (i) well. For part (ii), harmonic motion formula need to be careful when choosing to use sin or cos, and substituting initial conditions correctly - if in doubt derive via integration (either method was accepted, provided you set up the harmonic motion correctly). For part (iii), most students recognised that the particles didn't collide if the two equations didn't have a solution. This part was dependent on part (ii) and so was marked accordingly. If you used definite integrals, you need to ensure that the variable you are integrating against isn't one of the limits of the integral.
Q14 (b) - A correct diagram would help with this one. There are multiple ways to derive the result but the cosine angle formula (2 different ways) and using the equal angles of the equilateral triangle were the simplest.
Q14 (c) - Main piece of feedback is check you are actually reading all the parts of the question, including many students forgot their example had to satisfy, having an inverse and=f^{-1}(x)) . For the proof in part (ii), proof by contradiction as per solutions was the simplest method. (I've included some extra background on the definition of the inverse but this can be assumed). Part (iii) relied on using the previous parts so could be done even if you struggled to do part (i) and part (ii) by assuming the result was proven.
. For the proof in part (ii), proof by contradiction as per solutions was the simplest method. (I've included some extra background on the definition of the inverse but this can be assumed). Part (iii) relied on using the previous parts so could be done even if you struggled to do part (i) and part (ii) by assuming the result was proven.
I've posted more detailed markers notes for Q12 and Q14, and a set of solutions (not the official ones but ones I used heavily to mark with, so they may at times differ as they are based on the original set of questions (although I have since adjusted Q12(c), but I have cross checked against the official ones to make sure that they are correct but I may have made a latex error knowing me)
I will still have the question papers until the end of the week so if you want specific feedback send me a DM.
Q12: https://community.boredofstudies.or...mx2-trials-q12-solutions-markers-notes.20036/
Q14: https://community.boredofstudies.or...mx2-trials-q14-solutions-markers-notes.20037/
Some additional general comments/pointers:
Q12 (a) - Some students used a method more complicated then what was needed. Remember that for something to be even, you only need to show that it is or is not a multiple of 2M (where M is any choice of integer). If you did use cases and proof by contradiction for each, you needed to cover all cases even if it was just a cursory statement using W.L.O.G or similarly.
Q12 (b) - Students struggled with this question, expanding and then simplifying was the easiest approach and it was a test of patience and algebra skills. Main tip for this one, is to rework the formula to use the information given (in this case it could be used twice). Also check your solutions are valid (in fact only one student managed to get 2 marks, so close but forgot to eliminate spurious solutions that caused the cosec function to be undefined), its helpful to specify the range for variables in the question e.g.
Q12 (c) - Many people used the projection formula, to derive the result in part (i), but neglected to explain why they are using the formula (you did not need to use it for part (iii)). Diagrams were also helpful. In part (ii), students often had statements about the shortest distance that were insufficient to show that it was parallel (easiest way was to argue that they shared the same normal implied by an appropriate choice of the (x,y,z) vector, and comment on that the normal was orthogonal (perpendicular) for any choice of normal)
Q12 (d) - Generally this question was done well by all students. But when you setup IBP, don't use the DI table notation (with +/- as rows) that some students had employed as it is non standard notation and not very coherent. With the recursion in part (ii), make sure to evaluate the last term correctly (some students did not or did not show where the recursion ended).
Q14 (a) - Most students did part (i) well. For part (ii), harmonic motion formula need to be careful when choosing to use sin or cos, and substituting initial conditions correctly - if in doubt derive via integration (either method was accepted, provided you set up the harmonic motion correctly). For part (iii), most students recognised that the particles didn't collide if the two equations didn't have a solution. This part was dependent on part (ii) and so was marked accordingly. If you used definite integrals, you need to ensure that the variable you are integrating against isn't one of the limits of the integral.
Q14 (b) - A correct diagram would help with this one. There are multiple ways to derive the result but the cosine angle formula (2 different ways) and using the equal angles of the equilateral triangle were the simplest.
Q14 (c) - Main piece of feedback is check you are actually reading all the parts of the question, including many students forgot their example had to satisfy, having an inverse and
Last edited:

