How do you sketch
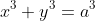
(where a is a constant)
using implicit differentiation?
this is from the Cambridge 3U book
Thanks!
This is actually more of an Extension 2 question:

Make y the subject of the expression:

Take the limit as x approaches infinity:

So we can see that as x approaches plus/minus infinity, the curve models the line y=-x. This implies that y=-x is an oblique asymptote.
We can verify this by subbing y=-x into our expression for the implicit derivative, which gives us:

We can also see from the implicit derivative that we have a horizontal tangent when:
)
Similarly for vertical tangents, we let the implicit derivative be infinity ie: the denominator is zero.
Using a similar method, we acquire an x intercept AND a vertical tangent at (a,0)
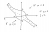
So from our information that we have deduced algebraically, we have the following diagram:
We observe that the equation of the curve is symmetrical ie: x --> y yields the same curve as y --> x
So we 'suspect' that the curve is symmetric about the line y=x (We can already sorta see it from the diagram!)
So let us solve the equation of the curve with the equation y = x to perhaps find this 'point of symmetry'. We will do so by letting y=x:

So adding this to our diagram, we have:
And that is our curve!
If you sketch the curve for a = 1, 2, 3, etc etc and superimpose them upon each other, you acquire the following contour curves for the surface:

And as you can see for all of them, they all have the asymptote y=-x.
Hope this helps.
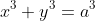 (where a is a constant)
(where a is a constant)