integral95
Well-Known Member
- Joined
- Dec 16, 2012
- Messages
- 779
- Gender
- Male
- HSC
- 2013
Re: HSC 2015 4U Marathon - Advanced Level
Well I dunno if this is too hard for the integration thread, but i'll post it here anyway.
From UNSW integration bee.
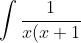(x+2)...(x+n)}\ \ dx )
Well I dunno if this is too hard for the integration thread, but i'll post it here anyway.
From UNSW integration bee.

