Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (1 Viewer)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
However the problem only arises for even numbers, that when we half it we get an odd number, so in this case, it will be 2, 6, 10.
We already disregard 2 so that doesnt matter, and we disregard 6 since it cancels out with arrangements with 12 anyway.
Look at 10 fruits being chosen, we can split it into 5 G, 5 A and no arrangement of 5 fruits can reflect this proportion. Hence we disregard that arrangement,
Hence 5726 - 5C2
But there is more to be excluded, we now look at numbers of fruits, such that we can separate them into groups of 3. i.e. multiples of 3:
3, 6, 9, 12
3, 6, 9 disregarded (odd numbers)
Look at 12: We can seperate it into 4 groups of 3, and no arrangement of 6 fruits can reflect this proportionality.
Hence 5726 - 5C2 - 5C4
Now lets check multiples of 4: 4, 8, 12
For 8: we can split into 2 groups of 4, however we can replicate this with 4, and same thing for 12, we can replicate this with 6. The reason being is that for 8, we seperate into 2 groups and 2 is a factor of 4 (whereas earlier 2 is not a factor of 5), and similarly for 12, 3 is a factor of 6.
Check multiples of 5: 5, 10
We already covered this. So the final answer which I hope to be right is:
5711
This problem only arises with choosing an even number of fruit, we will disregard the the situation with 6 fruits as you have mentioned as it will be reflected in 12 fruits and hence cancels out the arrangements anyway (but I get there is a problem).Sounds good
Hm ok... but what about the arrangement (3 grapes, 3 apples)? This is an arrangement for 6 fruits, and it's not proportional to any arrangement of 3 fruits , but yet it isn't legal...
You are almost therego deeper!
However the problem only arises for even numbers, that when we half it we get an odd number, so in this case, it will be 2, 6, 10.
We already disregard 2 so that doesnt matter, and we disregard 6 since it cancels out with arrangements with 12 anyway.
Look at 10 fruits being chosen, we can split it into 5 G, 5 A and no arrangement of 5 fruits can reflect this proportion. Hence we disregard that arrangement,
Hence 5726 - 5C2
But there is more to be excluded, we now look at numbers of fruits, such that we can separate them into groups of 3. i.e. multiples of 3:
3, 6, 9, 12
3, 6, 9 disregarded (odd numbers)
Look at 12: We can seperate it into 4 groups of 3, and no arrangement of 6 fruits can reflect this proportionality.
Hence 5726 - 5C2 - 5C4
Now lets check multiples of 4: 4, 8, 12
For 8: we can split into 2 groups of 4, however we can replicate this with 4, and same thing for 12, we can replicate this with 6. The reason being is that for 8, we seperate into 2 groups and 2 is a factor of 4 (whereas earlier 2 is not a factor of 5), and similarly for 12, 3 is a factor of 6.
Check multiples of 5: 5, 10
We already covered this. So the final answer which I hope to be right is:
5711
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 4U Marathon
Oops, sorry. Wasn't thinking carefully enough
Oops, sorry. Wasn't thinking carefully enough
Not always true. Picking 9 apples is proportional to picking 3 apples, for example.Let us establish the fact that if we pick an odd number of fruits, we cannot retain proportionality. Hence we keep all the odd numbered fruits arrangements (odd numbers above 6, I will get to this later)
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
 , I will have a go at it later:
, I will have a go at it later:
As for another question:
 ^n )
Oops, sorry. Wasn't thinking carefully enough
Not always true. Picking 9 apples is proportional to picking 3 apples, for example.
As for another question:
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon

I hope I've done this right considering it's 4am, I should be in bed argh.
Summing each one individually etc ends up with:, I will have a go at it later:
As for another question:
 ^n )
I hope I've done this right considering it's 4am, I should be in bed argh.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
This is correct, I am wondering what you mean by summing each individually, I was aiming at a geometric series differentiation approachSumming each one individually etc ends up with:
I hope I've done this right considering it's 4am, I should be in bed argh.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
^2 + \left ( \frac{1}{4} \right )^3 + \left ( \frac{1}{4} \right )^4 + ... \\\\ + \left ( \frac{1}{4} \right )^2 +\left ( \frac{1}{4} \right )^3 + \left ( \frac{1}{4} \right )^4 + ... \\\\ +\left ( \frac{1}{4} \right )^3 + \left ( \frac{1}{4} \right )^4 + ... \\\\ ... )
This is correct, I am wondering what you mean by summing each individually, I was aiming at a geometric series differentiation approach
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon

Differentiate:
x^{n-2}=\frac{-nx^{n-1}+(n-1)x^n+1}{(1-x)^2} )
Sub in x=1/4, then make n approach infinity, here we do assume that
And I probably should of stated that in the question.
+3(1/4)^2+... = \frac{1}{6/19} )
Multiply everything by 1/4
^n = 4/9 )
Well my working out was
Differentiate:
Sub in x=1/4, then make n approach infinity, here we do assume that
And I probably should of stated that in the question.
Multiply everything by 1/4
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
Last edited:
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 4U Marathon
Hope people don't mind that I'm not a 2013-er -- just trying to keep sharp over the holidays.
Solve for n:
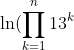 = 11325 \ln 13)
Hope people don't mind that I'm not a 2013-er -- just trying to keep sharp over the holidays.
Solve for n:
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
n = 150?Hope people don't mind that I'm not a 2013-er -- just trying to keep sharp over the holidays.
Solve for n:
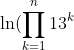 = 11325 \ln 13)
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 4U Marathon
Yep. Out of interest, what method did you use?n = 150?
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
)
Yep. Out of interest, what method did you use?
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
=\sum_{r=0}^{n} \frac{x^{r}}{r!} )
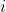 Show that E(x) does not have a double root$ \\ \\ $ii) Show that E(x) does not have any real roots if n is even$ )
No problem man.Hope people don't mind that I'm not a 2013-er -- just trying to keep sharp over the holidays.
Solve for n:
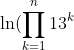 = 11325 \ln 13)
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
I've tried to do part (i) using a different approach than what you normally would, just to see if it works. Curious to see how justified this method is because I'm not sure lol:
First assume that there is a double root, that is:
 = (x-\alpha)^2Q(x)) for some root
for some root 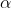
Differentiating both sides gives:
 = 2(x-\alpha)Q(x) + (x-\alpha)^2Q'(x))
Now it is obvious that:
 = E(x) - \frac{x^n}{n!})
So substituting this in gives:
 - \frac{x^n}{n!} = 2(x-\alpha)Q(x) + (x-\alpha)^2Q'(x))
Solving the following equations simulatenously:
 = (x-\alpha)^2Q(x))
 - \frac{x^n}{n!} = 2(x-\alpha)Q(x) + (x-\alpha)^2Q'(x))
By subtraction of the second from the first gives:
^2Q(x) - 2(x-\alpha)Q(x) - (x-\alpha)^2Q'(x))
[(x-\alpha)Q(x) - 2Q(x) - (x-\alpha)Q'(x)])
Now letting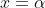 gives:
gives:

Hence:
 is a root of
is a root of )
But substituting this into) gives the result of
gives the result of 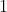
Hence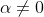
Now we have come to a contradiction, and hence our assumption must be wrong. That is,) does not have a double root.
does not have a double root.
No problem man.
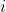 Show that E(x) does not have a double root$ \\ \\ $ii) Show that E(x) does not have any real roots if n is even$ )
I've tried to do part (i) using a different approach than what you normally would, just to see if it works. Curious to see how justified this method is because I'm not sure lol:
First assume that there is a double root, that is:
Differentiating both sides gives:
Now it is obvious that:
So substituting this in gives:
Solving the following equations simulatenously:
By subtraction of the second from the first gives:
Now letting
Hence:
But substituting this into
Hence
Now we have come to a contradiction, and hence our assumption must be wrong. That is,
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Nice work both of you:
As for a hint to the second part if anyone wants it, I have it in white here:
Consider E(alpha) where alpha is the stationary point of E(x) (this is how I proved it anyway)
Nice work both of you:
As for a hint to the second part if anyone wants it, I have it in white here:
Consider E(alpha) where alpha is the stationary point of E(x) (this is how I proved it anyway)
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 4U Marathon
The hint helped -- that question was (and still is) making me feel pretty stupid hope I didn't make a mistake here.
hope I didn't make a mistake here.
$, then $E'(\alpha) = 0$. But we established that $E'(x) = E(x) - \frac{x^n}{n!}$ so $E(\alpha) = \frac{\alpha^n}{n!} > 0$ as $n$ is even. So all stationary points of $E(x)$ are above the $x$-axis. Furthermore the double derivative $E''(\alpha) = E'(\alpha) - \frac{\alpha^{n-1}}{(n-1)!} = -\frac{\alpha^{n-1}}{(n-1)!}$ is negative for any negative $\alpha$ so this positive stationary point is a minimum if $\alpha$ is negative, and $E(x)$ is clearly monotonic increasing for positive values of $x$ and thus has no stationary points for these values. So $E(x)$ is always positive and thus has no real roots for even $n$. $)
The hint helped -- that question was (and still is) making me feel pretty stupid
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon

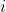 Show that $ \ \ y=e^x \ \ $is the only function which satisfies$ \ \ \ y'=y \ \ \ \ \ \fbox{1})
 Hence show that $ \\ \\ $If$ \ \ \ \ E(x) = \lim_{n \to \infty} \sum_{k=0}^{n} \frac{x^n}{n!} \\ \\ E(x) = e^x \ \ \ \ \ \fbox{2})
 You are given that $ \ \ \ \ y= \sin x \ \ \ \ y=\cos x \\ \\ $are the only functions which satisfy$ \ \ \ \ y'' + y =0 \\ \\ $Develop similar infinite power series to part ii for the sine and cosine functions$ \ \ \ \ \ \fbox{3})
 Hence show that$ \\ \\ e^{i\theta} = \cos \theta + i\sin \theta \ \ \ \ \ \ \fbox{4})
(probably a billion rigour issues with this)
Nice workThe hint helped -- that question was (and still is) making me feel pretty stupidhope I didn't make a mistake here.
$, then $E'(\alpha) = 0$. But we established that $E'(x) = E(x) - \frac{x^n}{n!}$ so $E(\alpha) = \frac{\alpha^n}{n!} > 0$ as $n$ is even. So all stationary points of $E(x)$ are above the $x$-axis. Furthermore the double derivative $E''(\alpha) = E'(\alpha) - \frac{\alpha^{n-1}}{(n-1)!} = -\frac{\alpha^{n-1}}{(n-1)!}$ is negative for any negative $\alpha$ so this positive stationary point is a minimum if $\alpha$ is negative, and $E(x)$ is clearly monotonic increasing for positive values of $x$ and thus has no stationary points for positive $\alpha$. So $E(x)$ is always positive and thus has no real roots for even $n$. $)
(probably a billion rigour issues with this)
- Status
- Not open for further replies.

