Re: MX2 2015 Integration Marathon
Alternatively, try the self-inverse substitution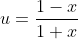
Alternatively, try the self-inverse substitution
Hint for others, exact value is a dead give away especially with zero at the lower limits.
Combine this with a clever substitution (trig).
Last edited:
