Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Integration Marathon (archive) (1 Viewer)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 2015 Integration Marathon
I think that's with seanieg's questionintegrand got the lower bound ages ago if you want to look for it by fowarding to when the question was posted
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
I hope people considered two cases ...... because of course √(1-cos²α) does not equal sinα.Alright lets see if this works:

Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
EDIT: shit...
why notI hope people considered two cases ...... because of course √(1-cos²α) does not equal sinα.
EDIT: shit...
Re: MX2 2015 Integration Marathon
Don't worry ... it still works for both cases. But not considering that is one mark off in an exam! ... unless there is another method which bypasses the issue.why not
EDIT: shit...
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
I made the answer based on the 1-c^2=s^2 fact so wouldnt that also make the answer wrongDon't worry ... it still works for both cases. But not considering that is one mark off in an exam!
Re: MX2 2015 Integration Marathon
So (ignoring all the extraneous rubbish):
2/sin(-α) times arctan sin(-α) = ....... ?
Inverse tan and sine are both odd functions.I made the answer based on the 1-c^2=s^2 fact so wouldnt that also make the answer wrong
So (ignoring all the extraneous rubbish):
2/sin(-α) times arctan sin(-α) = ....... ?
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: MX2 2015 Integration Marathon
So to summarise, if Q(n) is the quotient in the middle.
i) Show there are positive constants A,B such that A < Q(n) < B for all n. (My original question. You found a B, using the trapezoidal approximation, but can you find an A?)
ii) Show that Q(n) is monotone. (I just did this roughly, but I think it's not too hard.)
iii) Since the first two parts show that Q(n) -> c, you may assume this. Can you then find c? (This is distinct from i), you don't have to do it in an immediate sandwiching way, that sounds impossibly hard. Fortunately calculus gives us pretty powerful tools for computing things, especially when we don't have to worry about convergence!)
You don't need to find a lower bound of sqrt(2*pi) though, I just asked for any positive constant in my original question.I wasn't able to think of a way to approximate the lower bound as(though technically if you allow for a strict lower bound like 2pi as an answer to the question, then a strict lower bound of 1 would be sufficient too and easy to prove, though such a bound would not be useful).
How did you get it?
So to summarise, if Q(n) is the quotient in the middle.
i) Show there are positive constants A,B such that A < Q(n) < B for all n. (My original question. You found a B, using the trapezoidal approximation, but can you find an A?)
ii) Show that Q(n) is monotone. (I just did this roughly, but I think it's not too hard.)
iii) Since the first two parts show that Q(n) -> c, you may assume this. Can you then find c? (This is distinct from i), you don't have to do it in an immediate sandwiching way, that sounds impossibly hard. Fortunately calculus gives us pretty powerful tools for computing things, especially when we don't have to worry about convergence!)
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: MX2 2015 Integration Marathon
That was to seanieg89's question (I think an upper bound). And in the end, that exponent turned out to be the wrong one, so Integrand's bound wasn't very sharp. (Not that what he did was wrong.)integrand got the lower bound ages ago if you want to look for it by fowarding to when the question was posted
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
Pun intended ? sean said he was right tho ?That was to seanieg89's question (I think an upper bound). And in the end, that exponent turned out to be the wrong one, so Integrand's bound wasn't very sharp . (Not that what he did was wrong.)
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
BumpAlright lets see if this works:

glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: MX2 2015 Integration Marathon
As I said in brackets, the thing he wrote down wasn't untrue, it is just weaker than the result we can prove. Sean's original question was "wrong" in that the upper bound was easy to prove and the lower bound was hard to prove (impossible in fact, because it wasn't true lol). If you add 1 to both of the exponents the question makes sense though. (See my recent proof).
What pun? lol.Pun intended ? sean said he was right tho ?
As I said in brackets, the thing he wrote down wasn't untrue, it is just weaker than the result we can prove. Sean's original question was "wrong" in that the upper bound was easy to prove and the lower bound was hard to prove (impossible in fact, because it wasn't true lol). If you add 1 to both of the exponents the question makes sense though. (See my recent proof).
Re: MX2 2015 Integration Marathon
NEXT QUESTION:
I've seen this done already using indefinite integrals. But definite integrals seem to make things more fun and relaxing.

The latter integral was solved on the first page of this marathon (three different approaches are there).
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon

{{\frac{ln(\frac{1}{u})}{u^2+1}} )


ii)
EDIT: notsure how to fix this latex
i)Just gonna do one case. Assume sin(α)>0
NEXT QUESTION:
I've seen this done already using indefinite integrals. But definite integrals seem to make things more fun and relaxing.

ii)
EDIT: notsure how to fix this latex
Re: MX2 2015 Integration Marathon
Famous last words before a Pom gets his girlfriend pregnant.notsure how to fix this latex
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Re: MX2 2015 Integration Marathon
Whilst I'm here. Mega oh dear at the other comment.
EDIT: Yeah I figured you saw that.
Oh dear. But I'll take the 2I = \Int 0 part and say yeah you got it.i)
ii)
EDIT: notsure how to fix this latex
Whilst I'm here. Mega oh dear at the other comment.
EDIT: Yeah I figured you saw that.
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
Im using dummy variables i need to add the first I and the last I to let it =0 otherwise you lose a mark for fudging...Oh dear. But I'll take the 2I = \Int 0 part and say yeah you got it.
Whilst I'm here. Mega oh dear at the other comment.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: MX2 2015 Integration Marathon
My upper bound (for the log sum) came from the trapezoidal approximation (and the geometric observation that this approximation underestimates the integral of a concave function.)
My lower bound I did in a couple of ways.
i) We can in fact overestimate the integral of a concave function by integrating its tangent curve. A convenient (and in fact optimal, which you can test with differential calculus) way of bounding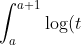\, dt) is by using the tangent at
is by using the tangent at 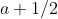 . If we then perform the integration of this tangent line (ie calculate the area of a trapezium lol), we get log(a+1/2). This is a tight enough upper bound to be able to sum such approximations and get an appropriate lower bound for the logsum.
. If we then perform the integration of this tangent line (ie calculate the area of a trapezium lol), we get log(a+1/2). This is a tight enough upper bound to be able to sum such approximations and get an appropriate lower bound for the logsum.
ii) We can study the trapezoidal approximation in a little more detail (wish we learned this in high school). Try to find a bound for the error of the trapezoidal approximation on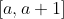 in terms of
in terms of 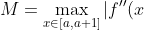|.) Then this means the trapezoidal bound is good enough, as we can overestimate the logintegral by (its trapezoidal sum) + (a partial sum of the basel series). Knowing that the latter is finite is good enough to get a lower bound for the logsum.
Then this means the trapezoidal bound is good enough, as we can overestimate the logintegral by (its trapezoidal sum) + (a partial sum of the basel series). Knowing that the latter is finite is good enough to get a lower bound for the logsum.
So did you end up having a proof that the Q(n) is bounded below by 1 Sy?You don't need to find a lower bound of sqrt(2*pi) though, I just asked for any positive constant in my original question.
So to summarise, if Q(n) is the quotient in the middle.
i) Show there are positive constants A,B such that A < Q(n) < B for all n. (My original question. You found a B, using the trapezoidal approximation, but can you find an A?)
ii) Show that Q(n) is monotone. (I just did this roughly, but I think it's not too hard.)
iii) Since the first two parts show that Q(n) -> c, you may assume this. Can you then find c? (This is distinct from i), you don't have to do it in an immediate sandwiching way, that sounds impossibly hard. Fortunately calculus gives us pretty powerful tools for computing things, especially when we don't have to worry about convergence!)
My upper bound (for the log sum) came from the trapezoidal approximation (and the geometric observation that this approximation underestimates the integral of a concave function.)
My lower bound I did in a couple of ways.
i) We can in fact overestimate the integral of a concave function by integrating its tangent curve. A convenient (and in fact optimal, which you can test with differential calculus) way of bounding
ii) We can study the trapezoidal approximation in a little more detail (wish we learned this in high school). Try to find a bound for the error of the trapezoidal approximation on
Last edited:
- Status
- Not open for further replies.
