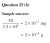2009 HSC (1 Viewer)
- Thread starter Yusra366
- Start date
We know that a sample of microbes with a mass of 50 mg contains 2.5 x 106 = 2 500 000 microbes. We also know that 1 mg is one one-thousandth of a gram.
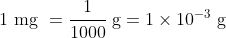

So, each microbe has a mass of 2.0 x 10-8 g (on average).
So, each microbe has a mass of 2.0 x 10-8 g (on average).
For Q28(d), we are tossing two dice and looking at the difference in the scores. It doesn't matter the order, so a "1" and a "6" and a "6" and a "1" both score 5. There are 36 possible results, summarised in the following diagram.

Since each of these 36 possible outcomes is equally likely, we can observe the frequencies and hence calculate the probabilities:
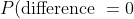 = \cfrac{6}{36} = \cfrac{1}{6})
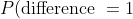 = \cfrac{10}{36} = \cfrac{5}{18})
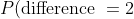 = \cfrac{8}{36} = \cfrac{2}{9})
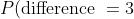 = \cfrac{6}{36} = \cfrac{1}{6})
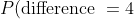 = \cfrac{4}{36} = \cfrac{1}{9})
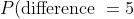 = \cfrac{2}{36} = \cfrac{1}{18})
Now, each time Juan did the experiment, he tossed the pair of dice 18 times. So, the expected outcomes (the number of times out of 18 that each difference should occur) can be found by multiplying each of the above probabilities by 18.
\ &= \cfrac{1}{6} \times 18 = 3 \\ E(\text{difference}\ = 1)\ &= \cfrac{5}{18} \times 18 = 5 \\ E(\text{difference}\ = 2)\ &= \cfrac{2}{9} \times 18 = 4 \\ E(\text{difference}\ = 3)\ &= \cfrac{1}{6} \times 18 = 3 \\ E(\text{difference}\ = 4)\ &= \cfrac{1}{9} \times 18 = 2 \\ E(\text{difference}\ = 5)\ &= \cfrac{1}{18} \times 18 = 1 \end{align*})
You can now compare this theoretical distribution of expected values with the actual values from Juan's experiments.

Since each of these 36 possible outcomes is equally likely, we can observe the frequencies and hence calculate the probabilities:
- There are 6 ways to achieve a difference of zero (the six "0" entries in the above table), and so
- There are 10 ways to achieve a difference of one (the ten "1" entries in the above table), and so
- There are 8 ways to achieve a difference of two (the eight "2" entries in the above table), and so
- There are 6 ways to achieve a difference of three (the six "3" entries in the above table), and so
- There are 4 ways to achieve a difference of four (the four "4" entries in the above table), and so
- There are 2 ways to achieve a difference of five (the two "5" entries in the above table), and so
Now, each time Juan did the experiment, he tossed the pair of dice 18 times. So, the expected outcomes (the number of times out of 18 that each difference should occur) can be found by multiplying each of the above probabilities by 18.
You can now compare this theoretical distribution of expected values with the actual values from Juan's experiments.
- Experiment 1 showed actual results of 3, 3, 2, 4, 3, 3 against an expectation of 3, 5, 4, 3, 2, 1, which shows differences (observed minus expected) of 0, -2, -2, +1, +1, +2.
- Experiment 1 showed actual results of 4, 4, 3, 3, 2, 2 against an expectation of 3, 5, 4, 3, 2, 1, which shows differences (observed minus expected) of +1, -1, -1, 0, 0, +1.
- The total of absolute differences for Experiment 1 is 8 whereas that for Experiment 2 is 4, meaning that the results from Experiment 1 show more deviation from the expected values than do the results from Experiment 2.
- No observed score in Experiment 2 is more than one away from its expectation, whereas Experiment 1 has three scores that are two away from their expectations.
- Only one of the scores in Experiment 1 matches its expectation, whereas two scores do so in Experiment 2.
- Taken collectively, the evidence supports Juan's conclusion that the Experiment 2 results are closer to what is expected for a pair of fair dice than are the Experiment 1 results.
Thank you sooo much for your help with both questions. It makes a lot more sense now. Really appreciate it!For Q28(d), we are tossing two dice and looking at the difference in the scores. It doesn't matter the order, so a "1" and a "6" and a "6" and a "1" both score 5. There are 36 possible results, summarised in the following diagram.
View attachment 32243
Since each of these 36 possible outcomes is equally likely, we can observe the frequencies and hence calculate the probabilities:
- There are 6 ways to achieve a difference of zero (the six "0" entries in the above table), and so
- There are 10 ways to achieve a difference of one (the ten "1" entries in the above table), and so
- There are 8 ways to achieve a difference of two (the eight "2" entries in the above table), and so
- There are 6 ways to achieve a difference of three (the six "3" entries in the above table), and so
- There are 4 ways to achieve a difference of four (the four "4" entries in the above table), and so
- There are 2 ways to achieve a difference of five (the two "5" entries in the above table), and so
Now, each time Juan did the experiment, he tossed the pair of dice 18 times. So, the expected outcomes (the number of times out of 18 that each difference should occur) can be found by multiplying each of the above probabilities by 18.
You can now compare this theoretical distribution of expected values with the actual values from Juan's experiments.
- Experiment 1 showed actual results of 3, 3, 2, 4, 3, 3 against an expectation of 3, 5, 4, 3, 2, 1, which shows differences (observed minus expected) of 0, -2, -2, +1, +1, +2.
- Experiment 1 showed actual results of 4, 4, 3, 3, 2, 2 against an expectation of 3, 5, 4, 3, 2, 1, which shows differences (observed minus expected) of +1, -1, -1, 0, 0, +1.
- The total of absolute differences for Experiment 1 is 8 whereas that for Experiment 2 is 4, meaning that the results from Experiment 1 show more deviation from the expected values than do the results from Experiment 2.
- No observed score in Experiment 2 is more than one away from its expectation, whereas Experiment 1 has three scores that are two away from their expectations.
- Only one of the scores in Experiment 1 matches its expectation, whereas two scores do so in Experiment 2.
- Taken collectively, the evidence supports Juan's conclusion that the Experiment 2 results are closer to what is expected for a pair of fair dice than are the Experiment 1 results.