Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
I recently came across a STEP question involving vectors in 3D Space, and a tetrahedron bound by a Sphere.
If we consider the points on the sphere which are the vertices of the regular tetrahedron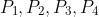
And consider the position vectors from O the origin corresponding to the above points respectively.
from O the origin corresponding to the above points respectively.
Before it really began the question it sort of assumed
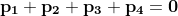
And I've been trying to prove it. So far I thought to express it in Spherical co-ordinate system.
As
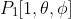
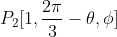
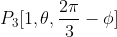
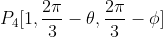
(Forgive the notation if it is incorrect)
Firstly, is this correct?
Then I tried to put it into 'cartesian' form, by applying that
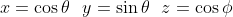
So I get 4 points in the form (x,y,z)
I add them all together and it doesn't give zero, what did I do wrong?
If we consider the points on the sphere which are the vertices of the regular tetrahedron
And consider the position vectors
Before it really began the question it sort of assumed
And I've been trying to prove it. So far I thought to express it in Spherical co-ordinate system.
As
(Forgive the notation if it is incorrect)
Firstly, is this correct?
Then I tried to put it into 'cartesian' form, by applying that
So I get 4 points in the form (x,y,z)
I add them all together and it doesn't give zero, what did I do wrong?
