Question 12
 \\ &= r^2\left(\theta - \cfrac{2\sin{\theta}\cos{\theta}}{2}\right) \\ &= r^2\big(\theta - \sin{\theta}\cos{\theta}\big) \end{align*})
From this, and noting that the radius

is constant, it follows that
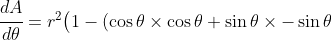\big) = r^2\big(1 - \cos^2{\theta} + \sin^2{\theta}\big))
Now, applying the Chain Rule repeatedly, we know that
 \end{align*})
And we already know
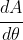
. The distance marked
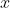
is the common side in a pair of congruent right-angled triangles (using the RHS test) and so that side bisects the angle
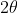
, and so
^2}} \\ &= -\cfrac{1}{r\sqrt{\cfrac{r^2 - x^2}{r^2}}} \\ &= -\cfrac{1}{\cfrac{r}{r}\sqrt{r^2 - x^2}} \\ &= -\cfrac{1}{\sqrt{r^2 - x^2}} \end{align*})
Combining these results, we know that
 \times -\cfrac{1}{\sqrt{r^2 - x^2}} \times \cfrac{dx}{dt} \\ &= \cfrac{r^2\big(\cos^2{\theta} - \sin^2{\theta} - 1\big)}{\sqrt{r^2 - x^2}} \times \cfrac{dx}{dt} \\ \text{Thus, when $\cfrac{dx}{dt} = -\sqrt{3}$ and $x = 1$, and given $r = 2$:} \qquad \cfrac{dA}{dt} &= \cfrac{2^2\big(\cos^2{\theta} - \sin^2{\theta} - 1\big)}{\sqrt{2^2 - 1^2}} \times -\sqrt{3} \\ &= \cfrac{4\sqrt{3}\big(1 - \cos^2{\theta} + \sin^2{\theta}\big)}{\sqrt{3}} \\ &= 4\big(1 - \cos^2{\theta} + \sin^2{\theta}\big) \\ &= 4\left[1 - \left(\cfrac{1}{2}\right)^2 + \sin^2{\theta}\right] \qquad \text{noting $\cos\theta = \cfrac{x}{r} = \cfrac{1}{2}$} \\ &= 4\left(1 - \cfrac{1}{4} + \cfrac{3}{4}\right) \qquad \text{noting $\cos^2\theta = \cfrac{1}{2} \implies \sin^2\theta = \cfrac{3}{4}$} \\ &= 4 - 1 + 3 \\ &= 6 \end{align*})