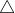Okay typing it up messed up and I just couldn't be bothered finding the mistake, so I just wrote it out. I didn't complete all the working out, but the rest is just algebra, and also realising that:
 = cis (2 \pi) = 1)
And you should eventually be able to show that:
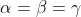
Which completes the proof that z1, z2 and z3 make an equilateral triangle.
However, the proof below is a bit long with the algebra towards the end. I will try to think of another one when I have time.
The alternative one I have in mind is obtained using the complex roots of unity for:
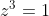
Then rotating all solutions by some arbitrary angle alpha, and show that it satisfies the given condition ie: z1 z2 and z3 make an equilateral triangle.
I also want to try to find a geometric interpretation of the condition there, so I can somehow relate it to some Circle Geometry theorem, which will facilitate the proof.
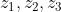 are distinct Complex no. and
are distinct Complex no. and 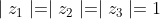
^2}+\frac{z_{2}z_{3}}{(z_{2}-z_{3})^2}+\frac{z_{3}z_{1}}{(z_{3}-z_{1})^2} = -1) .
. 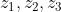 are the vertex of an equilateral
are the vertex of an equilateral