It's a little cumbersome to type out, (typesetting continued fractions is gruelling), but the basic idea can be summarised.
1. Chuck in x=-1 to the convergent Maclaurin series for e^x, this gives you an alternating series expression for e^(-1).
2. Find a finite continued fraction representation of a finite series like on Goldy's LHS but alternating. This comes from induction and the identity
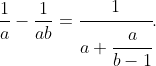
This lets us approximate 1-e^(-1) arbitrarily well by a finite continued fraction.
3. Notice what happens when you invert a continued fraction. The result comes from manipulating the continued fraction in 2. We invert, subtract 1, invert again, and add 1. This gives us the desired representation of e.
Note that we can't just subtract 1 from 1-e^(-1) and invert, because the continued fraction in question has no whole part outside the nested fractions, so subtraction is not easy (without getting negative numbers involved).