Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Maybe I can have a 'Cool Problem of the Day' sorta thing going...
A right angled triangle is inscribed within a circle such that all 3 vertices are on the circumference of the circle.
Given the ratio...
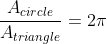
...where A_x denotes the area of x, find the other two angles of the triangle.
A right angled triangle is inscribed within a circle such that all 3 vertices are on the circumference of the circle.
Given the ratio...
...where A_x denotes the area of x, find the other two angles of the triangle.




