-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Equation of Tangent to Parabola (1 Viewer)
- Thread starter norez
- Start date
(1) solve simulateneously for (x,y) to find the point of contact.
i.e. rearrange x - 2y -2 = 0 in terms of y and subsubstite into x^2 = 16y.
This will be a quadratic equation and hence you can find the point of contact which turns out to be (4,1).
(2) Check the gradient of the curve y = 1/16 * x^2 evaulated at (4,1) is equal to the gradient of the line which is 1/2.
i.e. rearrange x - 2y -2 = 0 in terms of y and subsubstite into x^2 = 16y.
This will be a quadratic equation and hence you can find the point of contact which turns out to be (4,1).
(2) Check the gradient of the curve y = 1/16 * x^2 evaulated at (4,1) is equal to the gradient of the line which is 1/2.
hscishard
Active Member
There are heaps of ways.
Another method would be:
x(x1) = 2a(y+y1)
From x^2=16, a = 4
x(x1) = 8y + 8y1
x(x1) - 8y - 8y1 = 0
Divide by 4 on both sides. This matches the -2y in the given tangent.
(x1)x/4 - 2y -2y1 = 0
(x1)/4 = 1 (coefficient of x in x-2y-2=0)
x1 = 4
-2y1 = -2
y1= 1
This is after you proved that it's a tangent.
Another method would be:
x(x1) = 2a(y+y1)
From x^2=16, a = 4
x(x1) = 8y + 8y1
x(x1) - 8y - 8y1 = 0
Divide by 4 on both sides. This matches the -2y in the given tangent.
(x1)x/4 - 2y -2y1 = 0
(x1)/4 = 1 (coefficient of x in x-2y-2=0)
x1 = 4
-2y1 = -2
y1= 1
This is after you proved that it's a tangent.
random-1006
Banned
- Joined
- Jun 25, 2010
- Messages
- 988
- Gender
- Male
- HSC
- 2009
ahh i dont like that method, the easiest way would be to do:There are heaps of ways.
Another method would be:
x(x1) = 2a(y+y1)
From x^2=16, a = 4
x(x1) = 8y + 8y1
x(x1) - 8y - 8y1 = 0
Divide by 4 on both sides. This matches the -2y in the given tangent.
(x1)x/4 - 2y -2y1 = 0
(x1)/4 = 1 (coefficient of x in x-2y-2=0)
x1 = 4
-2y1 = -2
y1= 1
This is after you proved that it's a tangent.
-2y= 2-x
y= -1+(1/2)x
then do x^2= 16y
x^2 = 16 ( -1 +(1/2)x), then solve that quadratic ( you will see the discriminant is zero and you only get one root, ie a tangent)
thats the BEST, EASIEST and QUICKEST
hscishard
Active Member
LOL. Do you like this method?
x = 8t y=4t^2 (a = 4)
y= tx - at^2
2y=x-2
y=x/2 -1
t = 1/2
x = 8(1/2) = 4
y = 4(1/2)^2 = 1
x = 8t y=4t^2 (a = 4)
y= tx - at^2
2y=x-2
y=x/2 -1
t = 1/2
x = 8(1/2) = 4
y = 4(1/2)^2 = 1
random-1006
Banned
- Joined
- Jun 25, 2010
- Messages
- 988
- Gender
- Male
- HSC
- 2009
its not a bad method, but i still think my way was the best, your one involves memorising y= tx -at^2 ( you should be deriving these), and if you did derive it in the exam it would take longer than my wayLOL. Do you like this method?
x = 8t y=4t^2 (a = 4)
y= tx - at^2
2y=x-2
y=x/2 -1
t = 1/2
x = 8(1/2) = 4
y = 4(1/2)^2 = 1
random-1006
Banned
- Joined
- Jun 25, 2010
- Messages
- 988
- Gender
- Male
- HSC
- 2009
how about this METHOD!:
you put the two equations together and then find the discriminate. if it is zero, then the tangent forms a "double root" with that parabola!
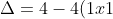=0$ $ $Hence, only one solution thus only cuts parabola once :D$)
that is the exact same as mine
