-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
heelllppp pls binomial q (1 Viewer)
- Thread starter yashbb
- Start date
icycledough
Well-Known Member
- Joined
- Aug 5, 2021
- Messages
- 784
- Gender
- Male
- HSC
- 2020
Can you help with this pls
Since x is to the power of 6, k has to equal three
Therefore the coefficient ofis 175000
20210920_135959.jpg
icycledough
Well-Known Member
- Joined
- Aug 5, 2021
- Messages
- 784
- Gender
- Male
- HSC
- 2020
Just to confirm, its number 3 yh? The one with the blue asterisk?
I've tried to solve it, but I haven't learnt any Ext 2 level projectile motion stuff yet. I'll try to learn it over the next few weeks if possible.Can you help with this pls
username_2
Active Member
- Joined
- Aug 1, 2020
- Messages
- 116
- Gender
- Male
- HSC
- 2020
So i remember doing this question and I couldn't figure it out then but I have now. I have put the solution down below. Anything you didn't understand, shoot a reply to this... here goes.



Ok so I would even think that many people will get up to this point. But here's the little trick - the keyword in the question is show:
You don't have to solve the equation to show that k = 0.158, you can just substitute in the value for LHS and RHS and check if this is a valid solution to the equation. (Btw there is no good manual way to solve this equation other than precise graphing but that is impossible in an exam). Hence, is my solution - ie the next steps - below. (This part might not be the best but do give suggestions about any other methods you might know)

Hope that is a bit more helpful!
Looking at @username_2's equation 1, and setting 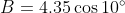 , we have:
, we have:
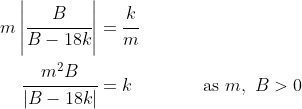
The solutions are thus the intersection of a diagonal line through the origin) and the absolute value of a hyperbola that has as its two asymptotes the
and the absolute value of a hyperbola that has as its two asymptotes the  -axis and
-axis and 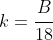 . There will likely be three solutions, one with
. There will likely be three solutions, one with 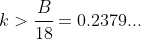 , and likely two between
, and likely two between 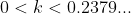 . We know we aren't looking for the solution above 0.2379..., so must be in the region where
. We know we aren't looking for the solution above 0.2379..., so must be in the region where 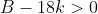 , and so can solve:
, and so can solve:
 \\ m^2B &= kB - 18k^2 \\ 18k^2 - kB + m^2B &= 0 \\ k &= \cfrac{-(-B) \pm \sqrt{(-B)^2 - 4(18)(m^2B)}}{2(18)} \\ k &= \cfrac{B \pm \sqrt{B^2 - 72m^2B}}{36} \\ &= \cfrac{4.2839... \pm \sqrt{4.2839...^2 - 72(0.145)^2 \times 4.2839...}}{36} \\ &= \cfrac{4.2839... \pm 3.4448...}{36} \\ &= 0.2146...\ \text{or}\ 0.023307... \end{align*})
The other solution, above 0.2379..., is in the region where 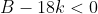 , and so can solve:
, and so can solve:
 \\ m^2B &= 18k^2 - kB \\ 18k^2 - kB - m^2B &= 0 \\ k &= \cfrac{-(-B) \pm \sqrt{(-B)^2 - 4(18)(-m^2B)}}{2(18)} \\ k &= \cfrac{B \pm \sqrt{B^2 + 72m^2B}}{36} \\ &= \cfrac{4.2839... \pm \sqrt{4.2839...^2 + 72(0.145)^2 \times 4.2839...}}{36} \\ &= \cfrac{4.2839... \pm 4.9836...}{36} \\ &= 0.2574...\ \text{or}\ -0.01943... \\ &\approx 0.257 \qquad \text{as $k > 0$} \end{align*})
So, the solution certainly can be found by HSC methods. There are indeed three solutions. And, either I have made an algebraic mistake(s) or there is a flaw in equation 1, as I haven't got 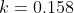 .
.
The solutions are thus the intersection of a diagonal line through the origin
username_2
Active Member
- Joined
- Aug 1, 2020
- Messages
- 116
- Gender
- Male
- HSC
- 2020
Hey... um its not m abs(B/(B-18k)) = k/m, its ln(abs(B/(B-18k))) = k/m. Sorry for the terrible handwritingLooking at @username_2's equation 1, and setting, we have:
The solutions are thus the intersection of a diagonal line through the originand the absolute value of a hyperbola that has as its two asymptotes the
-axis and
. There will likely be three solutions, one with
, and likely two between
. We know we aren't looking for the solution above 0.2379..., so must be in the region where
, and so can solve:
The other solution, above 0.2379..., is in the region where
, and so can solve:
So, the solution certainly can be found by HSC methods. There are indeed three solutions. And, either I have made an algebraic mistake(s) or there is a flaw in equation 1, as I haven't got
.
*That* explains my confusion!Hey... um its not m abs(B/(B-18k)) = k/m, its ln(abs(B/(B-18k))) = k/m. Sorry for the terrible handwriting
In that case, I agree that there is no reasonable way to solve the equation.
Though, for MX2, if we want to be rigorous, you might look at
and note that it is defined for


