Re: HSC 2018 MX2 Marathon
^m ) where
where 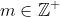
^m= 2m \cos \left(\frac{m\pi}{6}\right) + i\left(2m \sin\left(\frac{m\pi}{6}\right)\right) )
_____________________________________________________
If is real, then
is real, then 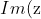 = 0 )
 &= 0 \\ \sin\left(\frac{m\pi}{6}\right) &= 0 \end{aligned} )
The smallest value of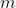 is
is 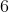 .
.
_____________________________________________________
If is purely imaginary, then
is purely imaginary, then 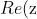 = 0 )
 &= 0 \\ \cos \left(\frac{m\pi}{6}\right) &= 0\end{aligned} )
The smallest value of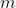 is
is 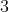 .
.
_____________________________________________________
If
The smallest value of
_____________________________________________________
If
The smallest value of
