A very easy way to work this question out is by replacing the terms
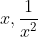
with
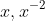
, next step is to start from the basics as in
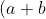^{2}=a^{2}+2ab+b^{2})
and as one can see it becomes
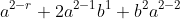
for your case it can we written for each of the terms it can be written as
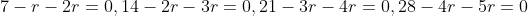
find the one that gives an integer value of r and there you are done. Note this is a common 2-3 marker question.
What I mean is this a 2 marker question would involve one to find the coefficient for a particular term or finding a constant term.
A 3 marker question would make you find the greatest coefficient and as such requires you to write
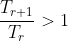
.
Another possible type of question that is a 2 marker would be the binomial theorem and they want you to do all sorts of things with it could be differentiating or say let x=1 as such which you could get
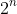
or whatever power.
To summarise there are too many different avenues for this topic. You can combine this with the topic of probability and make it an interesting question for candidates to encounter.