Four balls each with radius of 10 cm are placed on a table so that each one contacts two others. A fifth ball of the same size is placed on top of them so that it contacts all four balls. Find the distance from the top of the fifth ball to the table, expressing the answer in exact form .
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Measurement Question (Any hints would be great) (1 Viewer)
- Thread starter kpad5991
- Start date
Would the following working help?
Using the Pythagoras theorem:
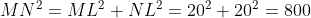
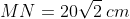
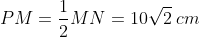
^2=200)
But we are calculating the distance from the top of the fifth ball to the table, meaning that we need to consider the length of the radius that goes north of point L and the length of one of the radii going south from M or N. Each of those radii are equal to 10 cm (given).
∴ The distance from the top to the table is:
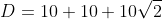
\:cm)
Using the Pythagoras theorem:
But we are calculating the distance from the top of the fifth ball to the table, meaning that we need to consider the length of the radius that goes north of point L and the length of one of the radii going south from M or N. Each of those radii are equal to 10 cm (given).
∴ The distance from the top to the table is:
Thank you so much. The answer says 20 + 10 root 2?Would the following working help?
View attachment 34849
Using the Pythagoras theorem:
∴ The distance from the top to the table is.
Apologies! There was a simple element in my working that I forgot to include! I have edited my initial reply to reflect the correct working.
Apologies! There was a simple element in my working that I forgot to include! I have edited my initial reply to reflect the correct working.
Hi Jimmy can you please help with these questions if possible:
1) Sally makes a cordial drink so that 10% of the drink is cordial concentration.. The rest is water. Sally has 350ml of the drink in a jug. She decided that she wants the concentrate to be only 8% of the drink. How much extra water does she need to add to the jug?
2) A diary farmer found that the milk supplied by his cows was 5% cream and 95% skimmed milk. How much skimmed milk he should add to a litre of milk to reduce the percentage of cream to 4%?
3) The cost of a car is reduced by 5% and then that price is then increased by 10%. The car now sells for $28 000. What was the original price of the car?
4) Natural fruit juice contains 80% water. In concentrating the juice, 75% of the water is removed. What is the percentage of water in the concentrated juice?
Thanks in advance
Okay I figured Q3 just the other 3
Regarding question 1, 350mL is comprised of 90% water (i.e. 315mL of water) and 10% cordial concentration (i.e. 35mL of water). We want the 35mL of cordial concentration to represent 8% of the drink instead of 10%, while keeping the actual amount of cordial concentration 35mL. This means that because we want 8% of the drink to consist of cordial concentration, water will now constitute 92% of the drink.
To do this:
To find out how much water has been added, you need to subtract 315 (the original amount of water) from the new amount of water, being 402.5mL, as follows:
Regarding question 2, we are required to reduce the cream to 4%. In a litre, 5% of cream means there are 50mL of cream 95% of skimmed milk means there are 950mL of skimmed milk. We want the 50mL of cream to consitute 4% instead 5%. Note that the 50mL (i.e. the actual amount remains unchanged).
If 50mL = 4%, how much mL is 96% of skimmed milk?
To do this:
1200mL is the amount of original skimmed milk in addition the amount of skimmed milk required to reduce cream to 4%.
To get the added component on its own, subtract the original amount of skimmed milk, as follows:
Regarding question 4, 80% water means that fresh juice is 20%. When 75% of 80% is removed, which is what happens when concentrating the juice, we get:
60 is the amount that we are subtracting from 80, leaving us with 20. Additionally, remember that fresh juice is 20%. Adding the fresh juice and the remaining water gives us:
Because 20 is half of 40, this means that the percentage of water in the concentrated juice is actually 50%, matching the answer for this question.