
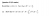
2 Questions:
1) is Q22 a) correct, because I'm under the impression it should be 100j (Instead of j) in the given equation
2) How exactly do you go about showing Q23? I imagine it is insufficient to show the integral approaches 0 as n approaches infinity, therefore there will always exist an n. I originally tried transforming the RHS to the integral of x^(r-1) from 1-0, but didn't know where to go from there.
Thanks

