This question is much more difficult than the above answers suggest, though I suspect that it is due to bad question writing. It highlights a more general issue, however, which is the hazards in making assumptions without noticing them, as they can be unjustified and sometimes render everything that follows as flawed.
Both the above answers have assumed that the four roots must be
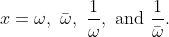
This
could be true, but it is not
necessarily true.
There is another possibility, which is that
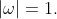
In this case:

Hence, the two demonstrated roots are themselves a conjugate pair as
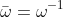
. The remaining two roots could then be:
- another conjugate pair; or,
- two distinct real roots; or,
- a single real double root.
A complete proof requires that these options be investigated and the required result either established as true or the option be demonstrated to be impossible. I suspect that the question means to exclude these possibilities, and so should define
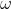
as a "non-real root of the equation where
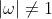
." Unfortunately, it doesn't.
MX2 students need to be very careful with unjustified assumptions and be vigilant in recognising when an assumption is being made.
Looking at one of these options (and leaving the others for others), the double real root case, can be shown to be impossible as the equation could then be factorised as
\left(x - \bar{\omega}\right)(x - k)^2 &= \left[x^2 - \left(\omega + \bar{\omega}\right)x + \omega\bar{\omega}\right]\left(x^2 - 2kx + k^2\right) \qquad \text{for some $k \in \mathbb{R}$} \\ &= \left(x^2 - 2\Re{(\omega)}x + |\omega|^2\right)\left(x^2 - 2kx + k^2\right) \\ & = \left(x^2 - 2\Re{(\omega)}x + 1\right)\left(x^2 - 2kx + k^2\right) \qquad \text{as $|\omega|^2 = 1$} \\ &= x^4 - 2\left(\Re{(\omega)} + k\right)x^3 + \left(1 + 4k\Re{(\omega)} + k^2\right)x^2 - 2k\left(1 + k\Re{(\omega)}\right)x + k^2 \end{align*})
in which case, by equating constants,
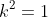
, and by equating coefficients of

and
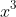
, it follows that
} + k\right) &= -2k\left(1 + k\Re{(\omega)}\right) \\ \Re{(\omega)} + k &= -k - k^2\Re{(\omega)} \\ \left(1 + k^2\right)\Re{(\omega)} &= -2k \\ \Re{(\omega)} &= -\frac{2k}{1 + k^2} \\ &= -\frac{2k}{1 + 1} = -k \qquad \text{since $k^2 = 1$} \\ &= \mp1 \qquad \text{as $k = \pm1$} \\ \\ \text{Hence,} \qquad b &= 2\left(\Re{(\omega)} + k\right) \\ &= 2\left(-k + k\right) \qquad \text{on using $\Re{(\omega)} = -k$} \\ &= 0 \end{align*})
This cannot be true as
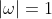
and
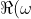} = \mp1)
requires
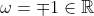
and so violates the requirement that
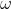
be a
non-real root of the equation.
In fact, this case gives
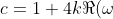} + k^2 = 1 + 4 \times \pm1 \times \mp1 + 1 = -2)
and so the equation is:
^2 &= 0 \\ (x + 1)^2(x - 1)^2 &= 0 \end{align*})
and the equation has only real roots, being two double roots at
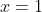
and
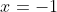
. The fact that the required identity is only true if
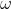
is chosen as
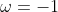
, yielding
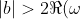} \qquad \implies \qquad 0 > -2)
but is untrue if
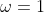
, is chosen as it yields the false statement that
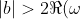} \qquad \implies \qquad 0 > 2)
is irrelevant as neither choice of
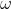
is valid.
I don't know if the claimed result is valid under the other options, or if those options are also impossible, but they need separate investigation to properly established either the truth of the proposition in the question or that the question is invalid without the case of
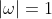
being excluded.
In this case:
. The remaining two roots could then be:
as a "non-real root of the equation where
." Unfortunately, it doesn't. MX2 students need to be very careful with unjustified assumptions and be vigilant in recognising when an assumption is being made.
, and by equating coefficients of
and
, it follows that
and
requires
and so violates the requirement that
be a non-real root of the equation.
and
. The fact that the required identity is only true if
is chosen as
, yielding
, is chosen as it yields the false statement that
is valid.
being excluded.

