Question:
A survey of 80 people with dark hair or brown eyes showed that 63 had dark hair and 59 had brown eyes. If one of the people surveyed is selected at random, what is the probability that the person will have:
a) dark hair but not brown eyes
b) both brown eyes and dark hair
c) brown eyes but not dark hair
Use 2 overlapping circles: B the left one for people with brown eyes and the right one, D, for those with dark hair. The overlapping section represents those who have brown eyes as well as dark hair. In elementary Set Theory, we refer to this as a Venn Diagram. The overlapping part is called ihe intersection of the sets B and D and is shown as or more simply BD for this question .
or more simply BD for this question .
Now let n(B) represent the number of people in set B - i.e. it is the number of people with brown eyes. Using a simple well-known formula in Set Theory:
No of people with brown eyes OR dark hair =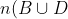 = n(B) + n(D) - n(BD) = 80 )
i.e. 59 + 63 - n(BD) = 80
.: n(BD) = 42.
So no of people with dark hair but not brown eyes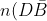 = 63 - 42 = 21)
No of people with brown eyes but not dark hair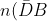 = 59 - 42 = 17)
So the requied probabilities are:
a)
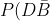 = \frac {21}{80} )
b)
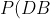 = \frac {42}{89} )
c)
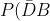 = \frac {17}{80} )
Of course for such a simple question, I need not have used all these Sets stuff.
A survey of 80 people with dark hair or brown eyes showed that 63 had dark hair and 59 had brown eyes. If one of the people surveyed is selected at random, what is the probability that the person will have:
a) dark hair but not brown eyes
b) both brown eyes and dark hair
c) brown eyes but not dark hair
Use 2 overlapping circles: B the left one for people with brown eyes and the right one, D, for those with dark hair. The overlapping section represents those who have brown eyes as well as dark hair. In elementary Set Theory, we refer to this as a Venn Diagram. The overlapping part is called ihe intersection of the sets B and D and is shown as
Now let n(B) represent the number of people in set B - i.e. it is the number of people with brown eyes. Using a simple well-known formula in Set Theory:
No of people with brown eyes OR dark hair =
i.e. 59 + 63 - n(BD) = 80
.: n(BD) = 42.
So no of people with dark hair but not brown eyes
No of people with brown eyes but not dark hair
So the requied probabilities are:
a)
b)
c)
Of course for such a simple question, I need not have used all these Sets stuff.
Last edited:

