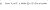-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Proofs (1 Viewer)
- Thread starter =)(=
- Start date
I'm gonna try using contrapositive, if that doesn't work, I'll try contradiction - give me like five mins lolView attachment 39718
I am not to sure how to go about this
edit: I HAVE NO CLUE HOW TO DO THIS
@synthesisFR @carrotsss calling in the backup
Last edited:
This is Wilson's TheoremView attachment 39718
I am not to sure how to go about this
https://en.wikipedia.org/wiki/Wilson's_theorem
well first off the question is wrong (p = 1 is a counterexample)View attachment 39718
I am not to sure how to go about this
but if we be generous and change ‘prime’ to ‘not composite’ then yes SadCeliac is right go by contrapositive: p is composite => p does not divide that thing
so p is composite, we can write it as p=ab, where 1<a<p
so (p-1)! is a multiple of a
so (p-1)! + 1 is not a multiple of a and so not a multiple of p.
that’s the basic outline - you just need to write it better.
Does that help?
also for the record this is not Wilson’s thm - Wilson’s thm is that AND that the converse is true. Proving the converse I believe is a much harder exercise [maybe can be done with strong induction? Not sure - haven’t tried] anyway this paragraph is irrelevant for 4U don’t worry about it
Exactly - I'll just clarify further but I think you got it.Ohh okay just to make sure (p-1)! is a multiple of a because there is a factor of a that makes it divisible by (p-1)!?
Because (p-1)! = (p-1)(p-2)...(a+1)(a)(a-1)...(3)(2)(1), which has a factor of a